同步发电机在滞后功率因数负载下的电枢反应

考虑图 1 所示的 2 极同步发电机。假设发电机负载为零功率因数滞后的感性负载。在这种情况下，相电流𝐼_𝑅、𝐼_𝑌和𝐼_𝐵将分别滞后于各自的相电压𝐸_𝑅、𝐸_𝑌和𝐸_𝐵 90°。同步发电机的相量图如图 2 所示。

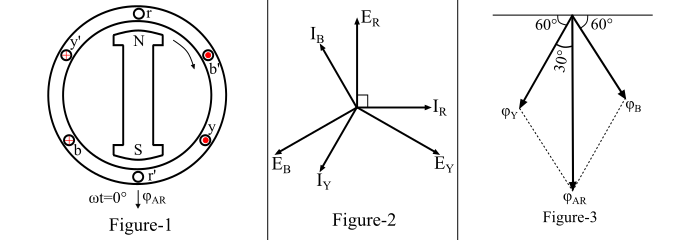
现在，在时间t = 0 时，电流和磁通的瞬时值由下式给出：

$$\mathrm{𝑖_{𝑅} = 0;\:\:φ_{𝑅} = 0}$$

$$\mathrm{𝑖_{𝑌} = 𝐼_{𝑚}\:sin(−120°) = −\frac{\sqrt{3}}{2}𝐼_{𝑚};\:\:\:φ_{𝑌} = −\frac{\sqrt{3}}{2}φ_{𝑚}}$$

$$\mathrm{𝑖_{𝐵} = 𝐼_{𝑚}\:sin(120°) = \frac{\sqrt{3}}{2}𝐼_{𝑚};\:\:\:φ_{𝐵} = \frac{\sqrt{3}}{2}φ_{𝑚}}$$

磁通的空间图如图 3 所示。根据平行四边形法则，合成的电枢反应磁通由下式给出：

$$\mathrm{𝜑_{𝐴𝑅} =\sqrt{φ^{2}_{𝑌} + φ^{2}_{B} + 2 φ_{𝑌}\:φ_{𝐵}\:cos\:60°}}$$

$$\mathrm{\Rightarrow\:φ_{𝐴𝑅} =\sqrt{(\frac{\sqrt{3}}{2}φ_{𝑚})^{2}+(\frac{\sqrt{3}}{2}φ_{𝑚})^{2}+2 \times (\frac{\sqrt{3}}{2}φ_{𝑚})\times (\frac{\sqrt{3}}{2}φ_{𝑚}) \times (\frac{1}{2})}}$$

$$\mathrm{∴\:𝜑_{𝐴𝑅} = 1.5\:φ_{𝑚}}$$

这里可以看出，电枢反应磁通φ_𝐴𝑅的方向与主磁场磁通相反。因此，它将反对并削弱主磁场磁通。电枢反应的这种效应称为去磁效应。同样，也可以证明，对于转子的连续位置，电枢反应磁通φ_𝐴𝑅的大小保持恒定，等于 1.5 𝜑_𝑚，并以同步速度旋转。此外，电枢反应磁通在每个相中感应的电动势滞后于各自的相电流 90°。

因此，当同步发电机以滞后功率因数供电时，电枢反应的效果部分是去磁的，部分是横向磁化的。

Manish Kumar Saini

更新于: 2021年9月25日

924 次浏览

启动您的 职业生涯

通过完成课程获得认证

开始学习