最经济的功率因数 – 定义、公式和示例

---

最经济的功率因数

使功率因数提高到能够获得最大净年节省的数值，称为最经济的功率因数。

当用户提高功率因数时，会导致其最大 kVA 需求减少。因此，在最大需求电费方面将有年度节省。尽管功率因数的改善涉及功率因数校正设备的资本投资，但用户每年仍将以年度利息和折旧的形式支出在用于功率因数校正的设备上进行的投资。因此，净年节省将等于最大需求电费的年节省减去功率因数校正设备的年支出。

推导

考虑一个用户在功率因数为 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 的情况下承受峰值负载 P kW，并且每年每 kVA 的最大需求电费为 Rs x。

假设用户借助功率因数校正装置将功率因数提高到 $\mathrm{cos}\, \phi _{\mathrm{2}}$。假设在功率因数改善装置上支出的费用为每年每 kVAR Rs y。

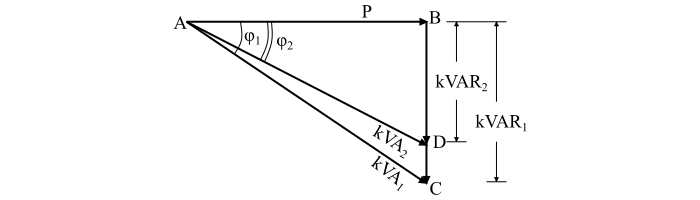
参考图示，初始功率因数 ($\mathrm{cos}\, \phi _{\mathrm{1}}$)下的功率三角形为 ABC，改进功率因数 ($\mathrm{cos}\, \phi _{\mathrm{2}}$)下的功率三角形为 ABD。

因此，原始功率因数下的最大 kVA 需求为：

$$\mathrm{\mathit{kV\, A_{\mathrm{1}}\mathrm{\, =\, }\frac{P}{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }P\, \mathrm{sec}\, \phi _{\mathrm{1}}}}$$

改进功率因数下的最大 kVA 需求由下式给出：

$$\mathrm{\mathit{kV\, A_{\mathrm{2}}\mathrm{\, =\, }\frac{P}{\mathrm{cos}\, \phi _{\mathrm{2}}}\mathrm{\, =\, }P\, \mathrm{sec}\, \phi _{\mathrm{2}}}}$$

然后，每年最大需求电费的节省为：

$$\mathrm{每年节省\mathrm{\, =\, } \mathit{Rs.x\left (kV\, A_{\mathrm{1}}-kV\, A_{\mathrm{2}} \right )}}$$

$$\mathrm{\Rightarrow 每年节省\mathrm{\, =\, } \mathit{Rs.x\left (\frac{P}{\mathrm{cos}\, \phi _{\mathrm{1}}}-\frac{P}{\mathrm{cos}\, \phi _{\mathrm{2}}} \right )}}$$

$$\mathrm{\Rightarrow 每年节省\mathrm{\, =\, } \mathit{Rs.xP\left (\mathrm{sec}\, \phi _{\mathrm{1}}- \mathrm{sec}\, \phi _{\mathrm{2}} \right )}\; \; \cdot \cdot \cdot \left ( 1 \right )}$$

此外，原始功率因数下的无功功率为：

$$\mathrm{kVAR_{\mathrm{1}}\mathit{\mathrm{\, =\, }P\, \mathrm{tan}\, \phi _{\mathrm{1}}}}$$

改进功率因数下的无功功率为：

$$\mathrm{kVAR_{\mathrm{2}}\mathit{\mathrm{\, =\, }P\, \mathrm{tan}\, \phi _{\mathrm{2}}}}$$

功率因数校正装置产生的超前无功功率由下式给出：

$$\mathrm{\mathrm{\, =\, }kVAR_{\mathrm{1}}-kVAR_{\mathrm{2}} \mathit{\mathrm{\, =\, }P \left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right )}}$$

因此，功率因数校正装置的年成本为：

$$\mathrm{设备年成本\mathrm{\, =\, }Rs\, \mathit{yP \left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right )}\: \: \cdot \cdot \cdot \left ( 2 \right )}$$

因此，根据公式 (1) 和 (2)，净年节省为：

$$\mathrm{\mathit{S\mathrm{\, =\, }xP\left (\mathrm{sec}\, \phi _{\mathrm{1}}- \mathrm{sec}\, \phi _{\mathrm{2}}\right )-yP\left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right )}}$$

现在，如果

$$\mathrm{\mathit{\frac{d\left ( S \right )}{d\, \phi \mathrm{2}}}\mathrm{\, =\, }0}$$

则净年节省将最大。

$$\mathrm{\Rightarrow \mathit{\frac{d}{d\, \phi _{\mathrm{2}}}\left [ xP\left (\mathrm{sec}\, \phi _{\mathrm{1}}- \mathrm{sec}\, \phi _{\mathrm{2}}\right )-yP\left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right ) \right ]}\mathrm{\, =\, }0}$$

$$\mathrm{\Rightarrow \mathit{P\left [ \frac{d}{d\, \phi _{\mathrm{2}}}\left ( x\, \mathrm{sec}\, \phi _{\mathrm{1}} \right )-\frac{d}{d\, \phi _{\mathrm{2}}}\left (x\, \mathrm{sec}\, \phi _{\mathrm{2}} \right )-\frac{d}{d\, \phi _{\mathrm{2}}}\left ( y\, \mathrm{tan}\, \phi _{\mathrm{1}} \right )\mathrm{\, +\, }\frac{d}{d\, \phi _{\mathrm{2}}}\left ( y\, \mathrm{tan}\, \phi _{\mathrm{2}} \right ) \right ]}\mathrm{\, =\, }0}$$

$$\mathrm{\Rightarrow 0-\mathit{x\, \mathrm{sec}\, \phi _{\mathrm{2}}\, \mathrm{tan}\, \phi _{\mathrm{2}}-\mathrm{0}\mathrm{\, +\, }y\, \mathrm{sec^{2}}\, \phi _{\mathrm{2}}}\mathrm{\, =\, }0}$$

$$\mathrm{\Rightarrow \mathit{\mathrm{tan}\, \phi _{\mathrm{2}}\mathrm{\, =\, }\frac{y}{x}\mathrm{sec}\, \phi _{\mathrm{2}}}}$$

$$\mathrm{\Rightarrow \mathit{\frac{\mathrm{tan}\, \phi _{\mathrm{2}}}{\mathrm{sec}\, \phi _{\mathrm{2}}}\mathrm{\, =\, }\mathrm{sin}\, \phi _{\mathrm{2}}\mathrm{\, =\, }\frac{y}{x}}}$$

因此，最经济的功率因数由下式给出：

$$\mathrm{\mathit{\mathrm{cos}\, \phi _{\mathrm{2}}\mathrm{\, =\, } \sqrt{\mathrm{1}-\mathrm{sin^{\mathrm{2}}}\, \phi _{\mathrm{2}}} \mathrm{\, =\, }\sqrt{\mathrm{1}-\left ( \frac{y}{x} \right )^{\mathrm{2}}} }\; \; \cdot \cdot \cdot \left ( 3 \right )}$$

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

根据公式 (3)，很明显，最经济的功率因数与原始功率因数无关。

数值示例

一家造纸厂的最大需求为 185 kW，功率因数为 0.8 滞后，每年每 kVA 的电费为 Rs 75。如果功率因数校正设备的成本为每 kVAR Rs 130。那么，工厂应以哪种最经济的功率因数运行？功率因数校正设备的利息和折旧费用为其资本投资的 10%。

解决方案

造纸厂的原始功率因数为：

$$\mathrm{\mathit{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }0.8 \, \, 滞后}$$

最大需求电费为

$$\mathrm{\mathit{x\mathrm{\, =\, }𝑅𝑠.}\,75\: 每\: kVA\: 每年 }$$

相位校正设备的支出为：

$$\mathrm{\mathit{y\mathrm{\, =\, }𝑅𝑠.}\,130\times 10\%\mathrm{\, =\, }\mathit{Rs.}\, 13\: 每\: kVA\: 每年 }$$

因此，工厂的最经济功率因数为：

$$\mathrm{\mathit{\mathrm{cos}\, \phi _{\mathrm{2}}\mathrm{\, =\, }\sqrt{\mathrm{1}-\left ( \frac{y}{x} \right )^{\mathrm{2}}}\mathrm{\, =\, }\mathrm{\sqrt{1-\left ( \frac{13}{75} \right )^{2}}}}}$$