数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究纠错码 - 低密度奇偶校验码
纠错码
纠错码 (ECC) 是一系列由特定算法生成的数字，用于检测和消除通过噪声信道传输的数据中的错误。纠错码确定已损坏位的精确数量以及损坏位的位置，并在算法的限制范围内。
ECC 可以大致分为两种类型：分组码和卷积码。低密度奇偶校验码 (LDPC) 是一种线性纠错分组码。它们适用于噪声很大的信道中的大块大小。
LDPC 码由 Robert G. Gallager 在 1960 年在麻省理工学院的博士论文中开发。因此，它们也被称为 Gallager 码。
低密度奇偶校验码的编码
低密度奇偶校验 (LFPC) 码由一个奇偶校验矩阵指定，该矩阵主要包含 0 和少量 1。矩阵的行表示方程，列表示码字中的位，即码符号。
LDPC 码由 表示，其中 是块长度， 是每列中 1 的数量， 是每行中 1 的数量，具有以下属性 -
j 是每列中 1 的数量，其中 j > 3
k 是每行中 1 的数量，其中 k > j。
示例 1 - 汉明码的奇偶校验矩阵
以下奇偶校验矩阵汉明码具有 ，其中 4 个信息位后跟 3 个偶校验位。校验位是对角线为 1。奇偶校验方程如下所示 -
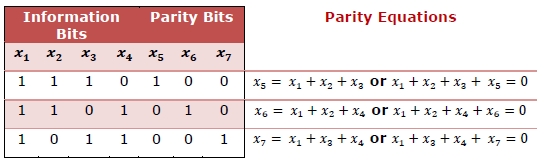
示例 2 - 低密度奇偶校验矩阵
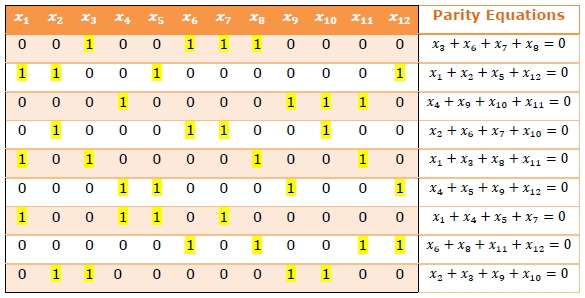
此示例说明了一个 (12, 3, 4) LDPC 矩阵，即 n = 12，j = 3 且 k = 4。这意味着每个方程对 4 个码符号进行运算，每个码符号出现在 3 个方程中。与汉明码的奇偶校验矩阵不同，此码在奇偶校验位中没有任何对角线 1。
LDPC 码的解码
LDPC 码有两种可能的解码技术 -
在第一种技术中，解码器根据奇偶校验方程执行所有奇偶校验。如果任何位包含超过固定数量的不满足奇偶校验方程，则该位的数值将反转。获得新值后，使用新值重新计算奇偶校验方程。重复此过程，直到所有奇偶校验方程都满足为止。
这种解码过程很简单，但仅适用于奇偶校验集较小的情况。
第二种方法对 LDPC 图执行概率算法。该图是一个稀疏二分图，包含两组节点，一组表示奇偶校验方程，另一组表示码符号。如果码符号存在于方程中，则一条线将第一组中的节点连接到第二组。解码是通过沿着图的线传递消息来完成的。消息从消息节点传递到校验节点，然后从校验节点传递回消息节点并计算其奇偶校验值。
这些方法的两个子类是置信传播和最大似然解码。尽管这些解码算法很复杂，但它们比前者产生更好的结果。
2K+ 浏览量
