纠错码中的汉明码

当我们考虑具有相同长度的两个码字时，汉明码可用于任何长度的数据单元。两个码字之间的汉明距离表示其特定项不同的位置数。

示例

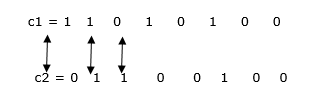
汉明距离为3。

汉明码也称为线性分组码。(n, k) 汉明码系列由 m 定义。

其中 m ≥ 3

最小距离_min = 3。
码率 = 码效率 = $\frac{k}{n} = \frac{2^{m}-m-1}{2^{m}-1} = 1 - \frac{m}{2^{m}-1}$ 当 m >> 1 时
则码率 r = 1，其中 k 是消息位，n 是每个分组传输的位数。

结构

奇偶校验（冗余）位插入到数据单元之间或数据单元的末尾。

为了评估，需要多个冗余位来准确表示给定的数据位数 m。我们应该找到 m 和 r 之间的关系。

如果总传输量为 m + r，则 r 必须表示 m + r + 1 个不同的状态。一个状态定义为无错误，m + r 个状态表示 m + r 个位置中每个位置的错误位置。

因此，r 位应发现 m + r + 1 个状态，而 r 位可以表示 2^r 个多个状态。所以 2^r ≥ m + r + 1。

假设 m = 7，则满足此方程式的最小 r 值为 4。

11	10	9	8	7	6	5	4	3	2	1
d	D	r₄	D	D	D	D	r₃	D	r₂	r₁

在这个 r 位放在 2ⁿ 位置上。例如，2⁰ = 1，2¹ = 2，2² = 4 等位置

在汉明码中，每个 r 位都是 VRC（垂直冗余校验）。

r₁ 位是通过使用所有二进制表示在最右位置包含 1 的位位置计算的，即 1, 3, 5, 7, 9, 11。

r₂ 位是通过使用在 2, 3, 6, 7, 10, 11 位置具有 1 的所有位置计算的，依此类推。r₃ 位将处理 4, 5, 6 位置的位。r₄ 在 8, 9, 10, 11 位置进行校验。

示例

1011

11 1001 0111 0101 0011 0001

r₄

r₃

r₂

r₁

r₂ 将负责它

1011 1010

11 10 0111 0110 0111 0010

r₆

r₄

r₂

r₁

等等。

计算 r 值

我们将原始字符的每个位放在 11 位单元的合适位置。我们可以计算多个位组合的偶校验。每个合并的校验值是相关 r 位的值。

示例

计算支持合并位 3、5、7、9、11 等的偶校验。最后 11 位代码通过传输线路发送。

Ginni

更新于：2021年5月5日

2K+ 次浏览

完成课程获得认证