数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学纠错码 - 里德-所罗门码
错误和纠错码
数据错误发生在数据位被破坏时。当位在计算机网络上传输时，由于干扰和网络问题，它们可能会被破坏，从而导致错误。
纠错码 (ECC) 是一系列由特定算法生成的数字，用于检测和纠正通过噪声信道传输的数据中的错误。纠错码在算法的限制范围内确定被破坏位的精确数量以及被破坏位的位置。
ECC 可以大致分为两种类型：分组码和卷积码。里德-所罗门码是一种分组码。
里德-所罗门码
里德-所罗门纠错码是最古老的编码之一，由 Irving S. Reed 和 Gustave Solomon 于 20 世纪 60 年代提出。它是非二进制 BCH 码的一个子类。BCH 码（Bose-Chaudhuri-Hocquenghem 码）是使用数据块上的多项式构造的循环 ECC。
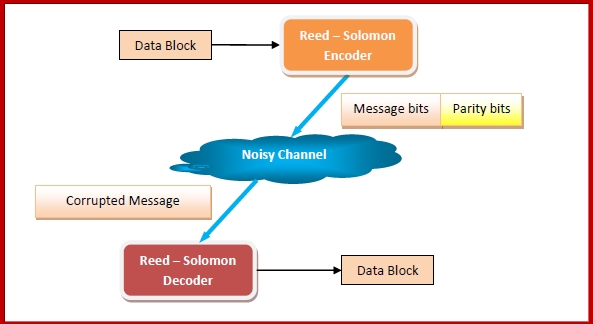
里德-所罗门编码器接收一个数据块，并在将其通过噪声信道传输之前添加冗余位（奇偶校验位）。接收数据后，解码器根据代码特性纠正错误。
里德-所罗门码的应用领域
主要的应用领域包括：
存储区域，如 CD、DVD、蓝光光盘
高速数据传输技术，如 DSL 和 WiMAX
高速调制解调器
二维码
广播系统，如卫星通信
存储系统，如 RAID 6
里德-所罗门码的参数
里德-所罗门码指定为 RS(n,k)。
这里，n 是块长度，以符号表示，满足关系 n = 2m - 1。
消息大小为 k 位。
因此，奇偶校验大小为 (n - k) 位
该码最多可以纠正码字中的 (t) 个错误，其中 (2t = n - k)。
下图显示了一个里德-所罗门码字：
里德-所罗门码的生成多项式
在使用分组码的编码系统中，有效的码字由可被另一个短长度的固定多项式整除的多项式组成。这个固定多项式称为生成多项式。
在里德-所罗门码中，构造具有因子的生成多项式，其中每个根都是伽罗瓦域中的连续元素。多项式的形式为：
g(x) = (x - α) (x - α2) (x - α3) ......(x - α2t) 其中 α 是一个本原元素。
使用里德-所罗门码进行编码
里德-所罗门码的编码方法包括以下步骤：
消息表示为多项式 p(x)，然后乘以生成多项式 g(x)。
消息向量 [x1,x2,x3.....xk] 映射到一个次数小于 k 的多项式，使得对于所有 i = 1,...k，px(αi) = xi。
使用拉格朗日插值等插值方法计算多项式。
使用此多项式，计算其他点 αk + 1....αn。
编码消息计算为 s(x) = p(x) * g(x)。发送方发送此编码消息以及生成多项式 g(x)。
使用里德-所罗门码进行解码
在接收端，执行以下解码过程：
接收机接收消息 r(x) 并将其除以生成多项式 g(x)。
如果 r(x)/g(x)=0，则表示没有错误。
如果 r(x)/g(x)≠0，则使用表达式 r(x) = p(x) * g(x) + e(x) 计算错误多项式。
错误多项式给出错误位置。
6K+ 浏览量
