数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究汉明码用于单错误纠正，双错误检测
汉明码是一种分组码，能够检测最多两个同时发生的比特错误并纠正单个比特错误。它是由 R.W. 汉明为纠错而开发的。
在这种编码方法中，源通过在消息中插入冗余位来对消息进行编码。这些冗余位是在消息本身中生成并插入到特定位置的额外位，以实现错误检测和纠正。当目标接收此消息时，它会执行重新计算以检测错误并找到出现错误的位位置。
汉明码用于单错误纠正
汉明码纠正单一错误的过程包括两部分，即发送端编码和接收端解码。
使用汉明码编码消息
发送方用于编码消息的过程包括以下步骤：
步骤 1 - 计算冗余位的数量。
步骤 2 - 确定冗余位的位置。
步骤 3 - 计算每个冗余位的值。
一旦将冗余位嵌入到消息中，就会将其发送到目标。
步骤 1 - 计算冗余位的数量。
如果消息包含 *m* 个数据位，则会向其添加 *r* 个冗余位，以便能够指示至少 *(m + r + 1)* 个不同的状态。这里，*(m + r)* 指示每个比特位置的错误位置，一个额外的状态指示没有错误。由于 *r* 个比特可以指示 *2r* 个状态，因此 *2r* 必须至少等于 *(m + r + 1)*。因此，以下等式应成立：
2r ≥ 𝑚 + 𝑟 + 1
**示例 1** - 如果数据为 7 位，即 *m = 7*，则满足上述等式的 *r* 的最小值为 4，(24 ≥ 7 + 4 + 1)。编码消息中的比特总数，*(m + r) = 11*。这被称为 (11,4) 码。
步骤 2 - 确定冗余位的位置。
将 *r* 个冗余位放置在 2 的幂次方的比特位置，即 1、2、4、8、16 等。在本文的其余部分中，它们被称为 *r1*（在位置 1）、*r2*（在位置 2）、*r3*（在位置 4）、*r4*（在位置 8）等等。
**示例 2** - 如果 *m = 7* 对应于 4，则冗余位的位置如下：
步骤 3 - 计算每个冗余位的值。
冗余位是奇偶校验位。奇偶校验位是一个额外的位，它使 1 的数量为偶数或奇数。两种类型的奇偶校验是：
**偶校验** - 这里消息中的比特总数变为偶数。
**奇校验** - 这里消息中的比特总数变为奇数。
每个冗余位 ri 根据其比特位置计算奇偶校验，通常是偶校验。它涵盖所有比特位置，其二进制表示在第 *ith* 位置包含 1，除了 *ri* 的位置。因此：
*r1 * 是所有数据位的奇偶校验位，其二进制表示在最低有效位包含 1，不包括 1（3、5、7、9、11 等）
*r2* 是所有数据位的奇偶校验位，其二进制表示在从右起第 2 位包含 1，不包括 2（3、6、7、10、11 等）
*r3* 是所有数据位的奇偶校验位，其二进制表示在从右起第 3 位包含 1，不包括 4（5-7、12-15、20-23 等）
**示例 3** - 假设消息 1100101 需要使用偶校验汉明码进行编码。这里，*m = 7* 并且 *r* 为 4。冗余位的值如下：
因此，发送的消息将是 11000101100。
汉明码消息解码
接收方收到传入消息后，会执行重新计算以检测错误并进行纠正。重新计算的步骤如下：
步骤 1 - 计算冗余位的数量。
步骤 2 - 确定冗余位的位置。
步骤 3 - 奇偶校验检查。
步骤 4 - 错误检测和纠正
步骤 1) 计算冗余位的数量
使用与编码中相同的公式，确定冗余位的数量。
2r ≥ 𝑚 + 𝑟 + 1
其中 *m* 是数据位的数量，*r* 是冗余位的数量。
步骤 2) 确定冗余位的位置
将 *r* 个冗余位放置在 2 的幂次方的比特位置，即 1、2、4、8、16 等。
步骤 3) 奇偶校验检查
根据数据位和冗余位使用与生成 c1、c2、c3、c4 等相同的规则计算奇偶校验位。因此
c1 = 奇偶校验(1、3、5、7、9、11 等)
c2 = 奇偶校验(2、3、6、7、10、11 等)
c3 = 奇偶校验(4-7、12-15、20-23 等)
步骤 4) 错误检测和纠正
计算奇偶校验位二进制值的十进制等价物。如果为 0，则没有错误。否则，十进制值给出出现错误的位位置。例如，如果 *c1c2c3c4* = 1001，则表示位置 9（1001 的十进制等价物）处的数位有错误。该位被翻转（从 0 变为 1 或从 1 变为 0）以获得正确的消息。
**示例 4** - 假设接收到的传入消息为 11110101101。
步骤 1 - 首先使用公式 2r ≥ m + r + 1 计算冗余位的数量。这里，m + r + 1 = 11 + 1 = 12。使得 2r ≥ 12 的 *r* 的最小值为 4。
步骤 2 - 冗余位的位置如下：
步骤 3 - 执行偶校验检查：
c1 = 偶校验(1、3、5、7、9、11) = 0
c2 = 偶校验(2、3、6、7、10、11) = 0
c3 = 偶校验(4、5、6、7) = 0
c4 = 偶校验(8、9、10、11) = 0
步骤 4 - 由于校验位 c1c2c3c4 的值为 0000 = 0，因此此消息中没有错误。
汉明码用于双错误检测
通过添加一个奇偶校验位作为 MSB（它是所有其他位的异或），可以修改汉明码以纠正单个错误并检测双错误。
**示例 5** - 如果我们考虑示例 3 中发送的码字 11000101100，在添加 P = 异或(1,1,0,0,0,1,0,1,1,0,0) = 0 后，要发送的新码字将是 011000101100。
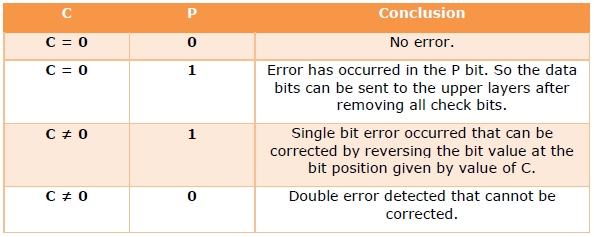
在接收端，错误检测如以下表格所示：
13K+ 次浏览
