偶数

---

引言

偶数是指可以被 2 整除的数，即形如 n = 2k 的数。数学是一门科学分支，其起源于人类在商业计算、了解数字之间关系、测量土地以及预测宇宙事件方面的需求。

数学被用作许多领域的重要工具，例如自然**科学、工程、医学、金融**和**社会科学**。应用数学涉及将数学应用于其他领域，以促进和应用新的科学发现。数学不仅包括数字及其运算（加法、减法、乘法、除法）以及形状（图形），更是一种随着科学研究及其应用不断发展的科学工具。

数字

• 数学中存在许多不同类型的数字。**自然数**(1, 2, 3, 4, . . . ) 是数字的基本示例。

• 用于表示数字的符号称为**数码**。可以假设，当人类学会在出生时数自己的手指时，就产生了数字的概念。**数字概念**的发展是数学的起源。

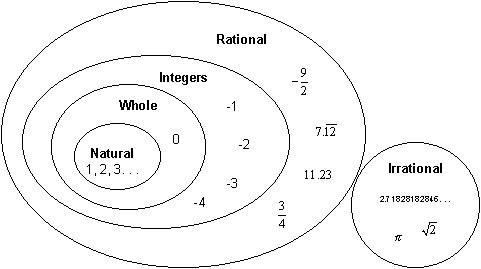
数系

自然数和整数

• 实践中最熟悉的数字，用于计数的数字，是**自然数**。

• 自然数定义为正整数序列 (1, 2, 3, 4, . . . )，而整数定义为非负整数序列 (0, 1, 2, 3, 4, . . . )。

整数

• 整数表示**正自然数**(1, 2, 3, 4, . . . )、它们的**负数**(-1, -2, -3, -4, . . . ) 和**零**。例如，13、9 和 -1204 是整数。

• 将**正数**和**负数**添加到自然数中形成了整数。

• **Z** 是用于表示整数集的符号。

有理数

• 分数或有理数，由分数表示的整数上下表示，例如**一半、四分之一**和**三分之一**，称为**有理数**。

• 此类数字用字母 Q 表示。

实数

• 直到 19 世纪，人类才毫无疑问地知道存在一个包含有理数 Q 并包含人们生活中遇到的所有数字的单一**超数集**{R}。

• 序列 {R} 的元素称为**实数**。在此，如果删除有理数，则剩余的数字称为无理数。

• 无理数有两种类型：**代数数**和**超越数**。

偶数

• 偶数是被 2 除后**没有余数**的数。**2 的倍数**都是偶数。

• 偶数是指最后一位数字可以是 0、2、4、6 或 8 的数。

• 例如，0、2、4、6、8、10、12、14、16、18 ……

偶数的性质

加法性质	减法性质	乘法性质
偶+偶=偶	偶-偶=偶	偶×偶=偶
偶+奇=奇	偶-奇=奇	偶×奇=偶
奇+偶=奇	奇-偶=奇	奇×偶=偶
奇+奇=偶	奇-奇=偶	奇×奇=奇

• 两个偶数或两个奇数的加法或减法运算结果为偶数。

• 任何偶数与任何奇数或偶数的乘法运算结果为偶数。

唯一的偶素数：2

• 素数是指大于 1 的自然数，除了**1 和自身**之外没有其他正因数。

• 1 和其他除了自身（除了 1）之外还有其他因数的自然数称为合数。例如，自然数 11 是一个素数。它除了 1 之外没有其他因数。

• 2 是唯一的**偶素数**，因为 2 的因数只有 1 和 2。它不能被任何其他数字整除。2 是最小的偶数。

偶数的代数

偶数也可以写成 $\mathrm{x\:=\:2n}$。因为任何数乘以 2 都得到偶数。这里 n 是正整数。但是奇数写成 $\mathrm{x\:=\:2n\:+\:1}$。如果 $\mathrm{n\:=\:3\:,\:x\:=\:2\times\:3\:=\:6}$。6 是偶数。

解题示例

1)如果两个数的和是 55，它们的差是 7，求这两个数。另外，求这两个数中哪个是偶数。

答案

设这两个数为 𝑥 和 𝑦。这里 $\mathrm{x\:>\:y}$

根据题意，

$$\mathrm{x\:+\:y\:=\:55\:\:\:\:\rightarrow\:(1)}$$

$$\mathrm{x\:-\:y\:=\:7\:\:\:\:\rightarrow\:(2)}$$

$$\mathrm{x\:=\:7\:+\:y\:\:\:\:\rightarrow\:(3)}$$

将 𝑥 的值代入方程 (1)

$$\mathrm{7\:+\:y\:+\:=\:55}$$

$$\mathrm{2y\:=\:55\:-\:7\:=\:48}$$

$$\mathrm{y\:=\:24}$$

将 y 的值代入方程 (3)

$$\mathrm{x\:=\:7\:+\:24\:=\:31}$$

因此 $\mathrm{31\:+\:24\:=\:55\:and\:31\:-\:24\:=\:7}$

这里 $\mathrm{y\:=\:24}$ 是偶数。因为 24 除以 2 后余数为零。

2)如果两个数的乘积是 27（奇数），这两个数的差是偶数。求这两个数。

答案

根据题意，

$\mathrm{x\times\:y\:=\:27\:,\:(x\:>\:y)}$

27 是一个合数。因为它可以被除了 1 和 27 之外的其他数整除。所以 𝑥 和 𝑦 的值为 9 和 3。因为 27 的因数是 1、3、9 和 27。根据题意，𝑥 - 𝑦 将是一个偶数。

因此，根据偶数的减法性质 $\mathrm{奇\:-\:奇\:=\:偶}$。9 和 3 是奇数。

$\mathrm{9\:-\:3\:=\:6}$ 。6 是偶数。

结论

数学是一门科学分支，其起源于人类在商业计算、了解数字之间关系、测量土地以及预测宇宙事件方面的需求。用于表示数字的符号称为数码。

数字概念的发展是数学的起源。偶数是被 2 除后没有余数的数。2 的倍数都是偶数。实践中最熟悉的数字，用于计数的数字，是自然数。将正数和负数添加到自然数中形成了整数。

常见问题

1. 复数是什么？

在数学中，复数是**实数和虚数的组合**。如果 a 和 b 表示两个实数，则复数 c 表示如下

$$\mathrm{c\:=\:a\:+\:bi}$$

2. 解释一下数制？

数制（或记数系统）是指**用于表示数字的书写系统**。也就是说，它是一种数学符号，以整数形式用数字或其他符号表示特定的数字集。

3. 什么是合数？

合数是**正整数**，除了自身和 1 之外，至少还有一个正因数（因子）。也就是说，合数可以认为是一个大于 1 的非素数正整数。

4. 什么是奇数？

奇数是最后一位数字为奇数的整数，例如 1、3、5、7、9。两个奇数的和与差相等，但乘积是奇数。

5. 定义集合？

集合是不同项目的集合或总和。虽然这可能看起来是一个非常简单的概念，但它是数学中最深刻的基本概念之一。集合中的组成部分称为元素。