数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学FIFO 推入重标记算法
FIFO 推入重标记算法是一种用于解决最大流问题的算法。
最大流问题是图论中的一个问题，我们需要找到可以通过互连的组件网络（例如管道、电线等）发送的资源或信息的最大流量，同时受到单个组件能够处理的容量限制。
换句话说，我们有一个 N 个节点的有向图。我们给定一个源节点和一个汇点。图中还有 M 条边，每条边都有一个权重，表示它能够处理的最大容量。我们需要找出可以在不超过任何边的容量的情况下从源节点传输到汇点的最大流量。
在第一种方法中，我们给定一个有向图 G，表示流量网络的边。每条边都有一个权重，表示该边的最大容量。我们最初将每条边的流量初始化为零。我们反复检查是否可以通过广度优先搜索将信息从源节点传输到汇点。只要有办法将信息从源节点传输到汇点，我们就传输该信息量并将其添加到最终答案中。我们还从所涉及的每条边的容量中减去它。
问题陈述
给定一个以有向图 G 形式表示的流量网络，以及表示每条边最大容量的边权重。我们需要找到可以从源节点传输到汇点的最大流量，条件是：
没有边的负载超过其容量。
到达一个节点的所有入边之和等于所有出边之和。
示例
输入
Source = 1, Sink = 4
输出
10
解释
我们可以从 1 流到 2 共 10 个单位，由于入边和出边必须具有相同的和，我们只能从 2 移动到 3 共 10 个单位，同样从 3 移动到 4 共 10 个单位。
输入
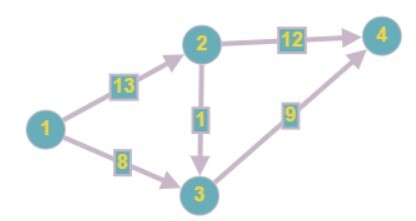
Source = 1, Sink = 4
输出
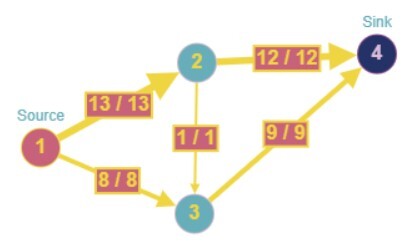
21
解释
输入
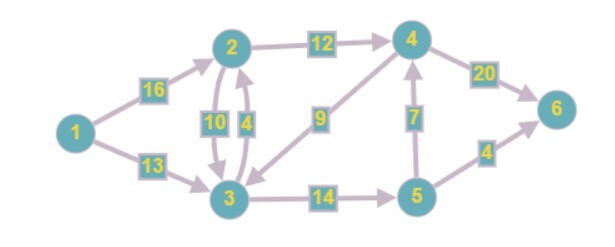
Source = 1, Sink = 6
输出
23
解释
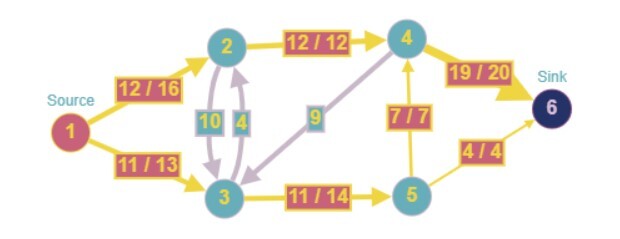
如上图所示，我们可以获得 23 的最大流量。
由于入边之和必须等于出边之和，并且顶点 4 的入边之和为 19，我们只能从边 4-6 流动 19 个单位，即使边的容量为 20。
方法
在这种方法中，我们给定一个有向图 G，表示流量网络的边。每条边都有一个权重，表示该边的最大容量。我们最初将每条边的流量初始化为零。我们反复检查是否可以通过广度优先搜索将信息从源节点传输到汇点。只要有办法将信息从源节点传输到汇点，我们就传输该信息量并将其添加到最终答案中。我们还从所涉及的每条边的容量中减去它。
算法
步骤 1.1 − 将所有边的初始流量设置为零。
步骤 1.2 − 为源节点分配一个等于网络中节点总数的高度。
步骤 1.3 − 计算源节点的剩余流量，即从源节点发出的所有边的容量之和。
步骤 2.1 − 在每个节点（不包括源节点和汇点）处，检查是否存在超过入流的剩余流量，以及是否存在高度比当前节点高度低一个单位的相邻节点。
步骤 2.2 − 如果上述条件为真，则沿边尽可能多地推送流量，并更新当前节点的剩余流量和边的总容量。
步骤 3.1 − 如果上述条件为假，则需要增加该节点的高度。
步骤 3.2 − 通过在其当前容量大于零的相邻节点的最小高度上加一来计算节点的新高度。
步骤 4.1 − 该算法使用先进先出 (FIFO) 队列来系统地管理要处理的节点，而不是反复扫描所有节点以查找潜在的推送和重标记。
步骤 4.2 − 检查步骤 2.1 中提到的条件后，我们将相邻节点推入队列。
步骤 5 − 该算法运行直到网络中没有节点从源节点获得任何剩余流量。满足此条件后，算法返回最大流量。
示例
#include <bits/stdc++.h>
using namespace std;
bool Can_push(vector<vector<int>> &Capacity, int source, int sink, vector<int> &parent) {
int N = Capacity.size();
vector<int> vis(N,0);
vis[source]=1;
parent[source]=-1;
queue<int> que;
que.push(source);
while(!que.empty()) {
int cnode = que.front();
que.pop();
for (int i=0;i<N;i++){
if (vis[i]==0 && Capacity[cnode][i] > 0){
vis[i] = 1;
parent[i] = cnode;
que.push(i);
}
}
}
if(vis[sink])return true;
return false;
}
int FIFOPushRelabel(vector<vector<int>> &Capacity, int source, int sink){
int N = Capacity.size();
vector<int> parent(N);
int max_flow = 0;
while(Can_push(Capacity,source,sink,parent)){
int curr_flow = INT_MAX;
int temp = sink;
while(temp!=source){
curr_flow = min(curr_flow,Capacity[parent[temp]][temp]);
temp = parent[temp];
}
temp = sink;
while(temp!=source){
Capacity[parent[temp]][temp]-=curr_flow;
temp = parent[temp];
}
max_flow+=curr_flow;
}
return max_flow;
}
int main() {
vector<vector<int>> Capacity = {
{0, 16, 13, 0, 0, 0},
{0, 0, 10, 12, 0, 0},
{0, 4, 0, 0, 14, 0},
{0, 0, 9, 0, 0, 20},
{0, 0, 0, 7, 0, 4},
{0, 0, 0, 0, 0, 0}
};
int source = 0, sink = 5;
cout<<FIFOPushRelabel(Capacity,source,sink);
return 0;
}
输出
23
时间复杂度 − O(V^3)，其中 V 是图中节点的数量。
空间复杂度 − O(V^2)，用于存储表示图的邻接矩阵。
197 次查看
