数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究找到一个节点，使得从该节点到所有叶子节点的路径都具有相同的颜色。
介绍
在数据结构中，一个最重要的难题是在树中找到一个节点，其中从该节点到叶子节点的所有路径都具有相同的颜色。本主题探讨如何利用图论和深度优先搜索方法快速找到这些节点。通过使用颜色编码方法并观察其对树遍历的影响，这个问题可以教会我们许多关于现实世界的知识，并帮助我们提高树相关过程的效率。
图论基础
图论是计算机科学和数学中最基本的概念之一。它研究实体之间的关系，这些关系以节点和边相连的形式表示。在这种情况下，图是由节点（点）和边（连接）组成的结构。这些图可以是有向图，其中每条边都指向一个特定的方向，也可以是无向图，其中连接可以双向进行。理解路径（由边连接的节点序列）和叶子节点（没有出边的节点）对于解决现实世界中遍历、连通性和结构问题至关重要。
理解树和DFS的概念
树是一种组织良好的数据结构，由通过边连接在一起的节点组成。树有一个根节点和从它分支出来的子节点。这形成了一个父子关系。与图不同，树不包含循环。它们在计算机科学中被广泛用于以最佳方式组织和表示信息。
深度优先搜索（DFS）是一种用于遍历图或树数据结构的算法。它从一个选定的节点开始，并尽可能地沿着每个分支向下遍历，然后再返回。它使用“后进先出”（LIFO）方法，通常使用堆栈来实现。DFS 用于查找路径、查找循环以及分析连接组件。
树的性质 - 树具有关键性质，例如深度（从根节点到节点的距离）、高度（树的最大深度）和度数（节点可以具有的子节点数）。除了根节点之外，每个节点都只有一个父节点，没有子节点的节点称为叶子节点。
性质 - 性质包括简单性、内存效率以及能够有效地找到从源节点到目标节点的路径。
颜色编码方案
算法设计中的一种常见做法是使用预定义的颜色集对树数据结构中的节点进行“着色”（或以其他方式识别）。对树的节点进行颜色编码可以更容易地识别趋势和其他特征。鉴于当前问题的性质，我们可以使用颜色编码方案通过查看所有通往该节点的路径是否具有相同的颜色来缩小目标节点范围。
在树中为节点着色 - 在将颜色编码方案应用于树之前，我们定义了节点着色的标准。例如，我们可以使用不同的颜色来表示具有偶数或奇数值的节点，或者根据节点在树中的级别使用不同的颜色。该过程涉及遍历树并根据所选标准为每个节点分配颜色。
理解颜色编码方案的工作原理 - 一旦树节点被着色，颜色编码方案就可以让我们快速检查从节点到叶子节点的给定路径是否为单色（所有节点都具有相同的颜色）。这是通过在树遍历和路径探索期间进行有效的颜色比较来实现的。该方案有助于识别满足所有通往叶子节点的路径都具有相同颜色的条件的节点，从而辅助搜索所需的节点。
查找所需的节点
为了找到一个节点，使得从该节点到所有叶子节点的路径都具有相同的颜色，我们使用一个利用颜色编码方案的系统算法。从根节点开始，我们遍历树，检查每个节点及其对应的颜色。我们探索从节点到叶子节点的路径，验证这些路径中的所有节点是否都具有相同的颜色。如果一个节点满足此条件，我们将其标记为所需节点的潜在候选者。算法持续进行，直到它搜索完整棵树或找到所需的节点。
分析时间和空间复杂度 - 算法的效率至关重要，尤其是在大型树的情况下。我们分析其时间复杂度，考虑诸如树的大小和颜色编码实现等因素。此外，我们评估空间复杂度，考虑颜色编码树和搜索过程中使用的任何辅助数据结构的存储需求。评估算法的复杂度有助于我们了解其性能特征和潜在的可扩展性，从而确保为当前问题提供有效的解决方案。
算法
// Function to check if all paths from a node to leaf nodes are of the same color
function findDesiredNodeWithSameColorPaths(node):
if node is null:
return null
// Explore the subtree rooted at 'node'
resultNode = exploreSubtree(node)
// If a node with the desired property is found, return it
if resultNode is not null:
return resultNode
// Otherwise, continue searching in the left subtree
return findDesiredNodeWithSameColorPaths(node.left) OR
findDesiredNodeWithSameColorPaths(node.right)
// Function to explore the subtree rooted at 'node'
function exploreSubtree(node):
if node is null:
return null
// Check if the path from 'node' to any leaf node is of the same color
if isMonochromaticPath(node, node.color):
return node
// Continue exploring in the left and right subtrees
leftResult = exploreSubtree(node.left)
rightResult = exploreSubtree(node.right)
// Return the first non-null result (if any)
return leftResult OR rightResult
// Function to check if the path from 'node' to any leaf node is of the same color
function isMonochromaticPath(node, color):
if node is null:
return true
// If the node's color doesn't match the desired color, the path is not monochromatic
if node.color != color:
return false
// Recursively check if both left and right subtrees have monochromatic paths
return isMonochromaticPath(node.left, color) AND
isMonochromaticPath(node.right, color)
图示
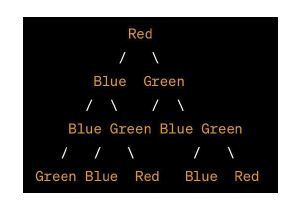
在这个二叉树的特定图示中，每个节点都以不同的颜色着色。红色表示根节点，蓝色表示左子节点，绿色表示右子节点。当我们向下遍历树时，每个左子节点的颜色从蓝色变为绿色，每个右子节点的颜色从绿色变为蓝色。
树底部的叶子节点将使用绿色、蓝色、绿色和红色着色。
二叉树通常使用颜色编码节点来表示，以便一目了然地查看其层次结构和模式。颜色编码可以帮助快速理解树的属性，这在许多树相关技术和应用中非常有用。
结论
总之，在树中找到一个节点，其中所有通往叶子节点的路径都具有相同颜色的问题在许多情况下都非常重要。通过使用颜色编码和快速遍历树，这种方法是查找满足给定条件的节点的强大方法。
197 次查看
