数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究在 C++ 中打印给定节点距离 K 的所有节点
在这个问题中，我们给定一棵二叉树、一个目标节点和一个整数 K。我们必须打印树中所有与目标节点距离为 K 的节点。
二叉树是一种特殊的树，其每个节点最多有两个子节点（一个/两个/零个）。
让我们举一个例子来理解这个问题
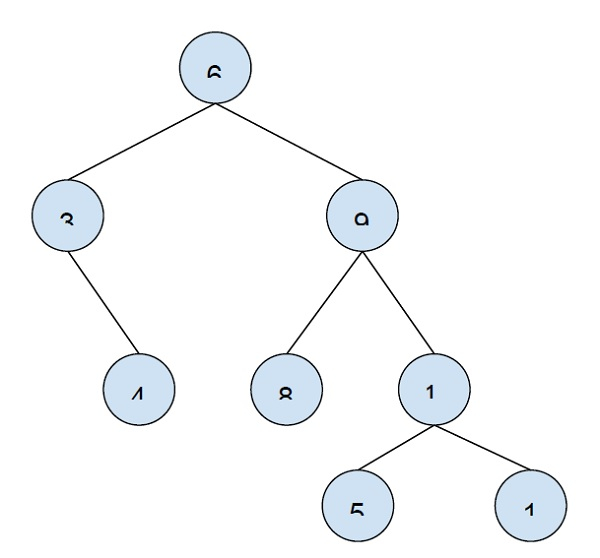
K = 2
目标节点：9
输出 -
5 1 3.
解释 -
节点的距离可以向上、向下或在同一层级上计算。因此，我们将相应地返回节点。
为了解决这个问题，我们必须理解与目标节点距离为 K 的节点的类型。
从上面的例子中，我们可以看到距离为 k 的节点可能位于目标节点的子树中（5 和 1），或者位于目标节点的祖先节点（3）的子树中的任何位置。
现在，解决第一种情况的方法是遍历目标节点的子树，并检查节点与目标节点的距离是否为 K。如果是，则打印该节点。
对于第二种情况，我们必须检查祖先节点以及这些祖先节点的子树，以找到目标节点，并打印所有与它距离为 K 的节点。
下面的程序将展示我们解决方案的实现 -
示例
#include <iostream>
using namespace std;
struct node {
int data;
struct node *left, *right;
};
void printSubtreeNodes(node *root, int k) {
if (root == NULL || k < 0) return;
if (k==0){
cout<<root->data<<"\t";
return;
}
printSubtreeNodes(root->left, k-1);
printSubtreeNodes(root->right, k-1);
}
int printKNodes(node* root, node* target , int k){
if (root == NULL) return -1;
if (root == target){
printSubtreeNodes(root, k);
return 0;
}
int dl = printKNodes(root->left, target, k);
if (dl != -1){
if (dl + 1 == k)
cout<<root->data<<"\t";
else
printSubtreeNodes(root->right, k-dl-2);
return 1 + dl;
}
int dr = printKNodes(root->right, target, k);
if (dr != -1){
if (dr + 1 == k)
cout << root->data << endl;
else
printSubtreeNodes(root->left, k-dr-2);
return 1 + dr;
}
return -1;
}
node *insertNode(int data){
node *temp = new node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
int main(){
node * root = insertNode(6);
root->left = insertNode(3);
root->right = insertNode(9);
root->left->right = insertNode(4);
root->right->left = insertNode(8);
root->right->right = insertNode(10);
root->right->right->left = insertNode(5);
root->right->right->right = insertNode(1);
node * target = root->right;
int K = 2;
cout<<"Nodes at distance "<<K<<" from the target node are :\n";
printKNodes(root, target, K);
return 0;
}输出
Nodes at distance 2 from the target n tode are − 5 1 3
更新于：2020年1月22日
417 次查看
广告