数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在 C++ 中查找给定集合中每个节点可到达的所有节点
假设我们有一个无向图和一组顶点；我们必须找到给定集合中每个顶点可到达的所有节点。
因此，如果输入类似于
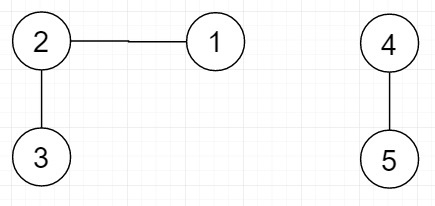
则输出将为 [1,2,3] 和 [4,5]，因为它们是两个连通分量。
为了解决这个问题，我们将遵循以下步骤 -
- nodes := 图中的节点数
- 定义一个大小为：nodes+1 的数组 visited。并填充 0
- 定义一个映射 m
- comp_sum := 0
- 初始化 i := 0，当 i < n 时，更新（i 增加 1），执行 -
- u := arr[i]
- 如果 visited[u] 为假，则 -
- (comp_sum 增加 1)
- m[visited[u]] := 从节点 u 开始对 g 进行广度优先搜索遍历，同时计算 comp_sum
- 打印 m[visited[u]] 的遍历结果
示例
让我们看看以下实现以获得更好的理解 -
#include <bits/stdc++.h>
using namespace std;
class Graph{
public:
int nodes;
list<int> *adj_list;
Graph(int);
void insert_edge(int, int);
vector<int> BFS(int, int, int []);
};
Graph::Graph(int nodes) {
this->nodes = nodes;
adj_list = new list<int>[nodes+1];
}
void Graph::insert_edge(int u, int v) {
adj_list[u].push_back(v);
adj_list[v].push_back(u);
}
vector<int> Graph::BFS(int comp_sum, int src,int visited[]){
queue<int> queue;
queue.push(src);
visited[src] = comp_sum;
vector<int> reachableNodes;
while(!queue.empty()) {
int u = queue.front();
queue.pop();
reachableNodes.push_back(u);
for (auto itr = adj_list[u].begin(); itr != adj_list[u].end(); itr++) {
if (!visited[*itr]) {
visited[*itr] = comp_sum;
queue.push(*itr);
}
}
}
return reachableNodes;
}
void displayReachableNodes(int n, unordered_map <int, vector<int> > m) {
vector<int> temp = m[n];
for (int i=0; i<temp.size(); i++)
cout << temp[i] << " ";
cout << endl;
}
void get_all_reachable(Graph g, int arr[], int n) {
int nodes = g.nodes;
int visited[nodes+1];
memset(visited, 0, sizeof(visited));
unordered_map <int, vector<int> > m;
int comp_sum = 0;
for (int i = 0 ; i < n ; i++) {
int u = arr[i];
if (!visited[u]) {
comp_sum++;
m[visited[u]] = g.BFS(comp_sum, u, visited);
}
cout << "Reachable Nodes from " << u <<" are\n";
displayReachableNodes(visited[u], m);
}
}
int main() {
int nodes = 5;
Graph g(nodes);
g.insert_edge(1, 2);
g.insert_edge(2, 3);
g.insert_edge(4, 5);
int arr[] = {2, 4, 1};
int n = sizeof(arr)/sizeof(int);
get_all_reachable(g, arr, n);
}输入
g.insert_edge(1, 2); g.insert_edge(2, 3); g.insert_edge(4, 5);
输出
Reachable Nodes from 2 are 2 1 3 Reachable Nodes from 4 are 4 5 Reachable Nodes from 1 are 2 1 3
更新于: 2020-08-28
558 次查看
广告