数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究向给定 BST 中的每个节点添加所有较大的值
在此，我们将看到一个有趣的问题，其中我们将向给定的二叉搜索树中的每个节点添加较大的值。因此，初始树和最终树如下图所示：
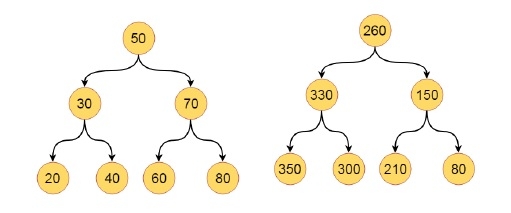
算法
bstUpdate(root, sum) -
Begin if root is null, then stop bstUpdate(right of room, sum) sum := sum + value of root update root value using sum bstUpdate(left of room, sum) End
示例
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node *getNode(int item) {
Node *newNode = new Node();
newNode->data = item;
newNode->left = newNode->right = NULL;
return newNode;
}
void updateBST(Node *root, int *sum) {
if (root == NULL)
return;
updateBST(root->right, sum); //update right sub tree
*sum = *sum + root->data;
root->data = *sum; //update root data
updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
int sum = 0;
updateBST(root, &sum);
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
Node* insert(Node* node, int data) {
if (node == NULL)
return getNode(data);
if (data <= node->data) //go to left
node->left = insert(node->left, data);
else //go to right
node->right = insert(node->right, data);
return node;
}
int main() {
int data[] = {50, 30, 20, 40, 70, 60, 80};
int n = sizeof(data)/sizeof(data[0]);
Node *root = NULL;
for(int i = 0; i < n; i++) {
root = insert(root, data[i]);
}
BSTUpdate(root);
inorder(root);
}输出
350 330 300 260 210 150 80
更新于：20-8-2019
110 次浏览
广告