数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会学科
时尚研究
法律研究用 C++ 打印二叉树中两给定层次之间的所有节点
在这个问题中，我们给定一个二叉树和树中的两个层次（上层和下层），并且必须打印该树上层和下层之间的所有节点。
二叉树是一种特殊树，其每个节点最多有两个节点（一个/两个/没有）。
让我们举个例子来理解这个问题 −
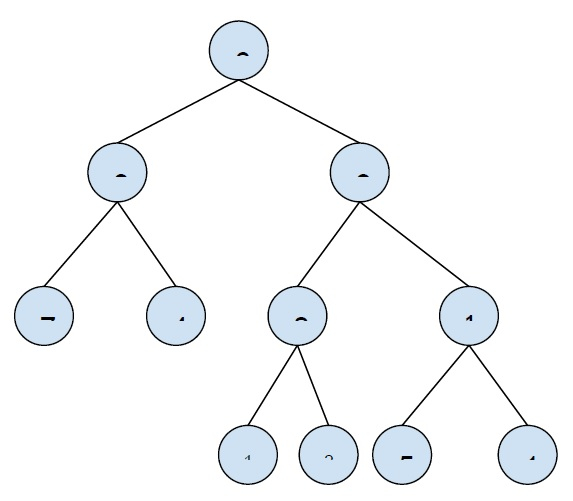
上层 − 1
下层 − 3
输出 −
6 3 9 7 4 8 10
为了解决这个问题，我们必须打印树中特定层次的节点。我们将使用一个循环从树中的上层 到下层 调用递归函数。
此算法很简单但是更复杂，顺序为 n2 。
一种更有效的解决方案是执行中序遍历并使用队列。并打印给定的上层和下层内的节点。
实现我们解决方案的程序 −
示例
#include <iostream>
#include <queue>
using namespace std;
struct Node{
int key;
struct Node* left, *right;
};
void printNodesAtLevel(Node* root, int low, int high){
queue <Node *> Q;
Node *marker = new Node;
int level = 1;
Q.push(root);
Q.push(marker);
while (Q.empty() == false){
Node *n = Q.front();
Q.pop();
if (n == marker){
cout << endl;
level++;
if (Q.empty() == true || level > high) break;
Q.push(marker);
continue;
}
if (level >= low)
cout<<n->key<<" ";
if (n->left != NULL) Q.push(n->left);
if (n->right != NULL) Q.push(n->right);
}
}
Node* insertNode(int key){
Node* temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return (temp);
}
int main() {
struct Node *root = insertNode(6);
root->left = insertNode(3);
root->right = insertNode(9);
root->left->left = insertNode(7);
root->left->right = insertNode(4);
root->left->right->left = insertNode(8);
root->left->right->right = insertNode(10);
root->left->right->right->left = insertNode(5);
root->left->right->right->right = insertNode(1);
root->left->right->left->left = insertNode(14);
root->left->right->left->right = insertNode(26);
int upper = 3;
int lower = 1;
cout << "Level wise Nodes between level "<<lower<<" and "<<upper<<" are \n";
printNodesAtLevel(root, lower, upper);
return 0;
}输出
Level wise Nodes between level 1 and 3 are 6 3 9 7 4
更新于：22-Jan-2020
161 浏览次数
广告