数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究以 C++ 编程输出二叉树中所有节点的级别。
在二叉树中，任务是从 1 到 n 为存储在节点中的每个键打印关联的级别
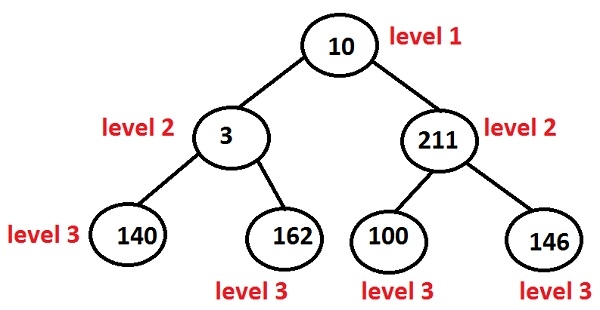
在上面的树中，节点为 -
10 at level 1 3 and 211 at level 2 140, 162, 100 and 146 at level 3
给定密钥，程序必须打印该特定密钥的级别。
示例
Input: 10 3 211 140 162 100 146 Output: level of 10 is 1 Level of 3 is 2 Level of 211 is 2 Level of 140 is 3 Level of 162 is 3 Level of 100 is 3 Level of 146 is 3
算法
START
Step 1 -> create a structure of a node as
struct node
struct node *left, *right
int data
End
Step 2 -> function to create a node
node* newnode(int data)
node *temp = new node
temp->data = data
temp->left = temp->right= NULL
return temp
step 3 -> create function for finding levels of a node
void levels(Node* root)
IF root=NULL
Return
End
Create STL queue<pair<struct Node*, int> >que
que.push({root, 1})
create STL pair<struct Node*, int> par
Loop While !que.empty()
par = que.front()
que.pop()
print par.first->data and par.second
IF par.first->left
que.push({ par.first->left, par.second + 1 })
END
IF par.first->right
que.push({ par.first->right, par.second + 1 })
End
End
STOP示例
#include <bits/stdc++.h>
using namespace std;
//structure of a node
struct Node{
int data;
struct Node *left, *right;
};
//it will print levels of a tree
void levels(Node* root){
if (root==NULL)
return;
queue<pair<struct Node*, int> >que;
que.push({root, 1});
pair<struct Node*, int> par;
while (!que.empty()) {
par = que.front();
que.pop();
cout << "Level of " << par.first->data << " is " << par.second << "\n";
if (par.first->left)
que.push({ par.first->left, par.second + 1 });
if (par.first->right)
que.push({ par.first->right, par.second + 1 });
}
}
//function to create nodes annd hence generate tree
Node* newnode(int data){
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
int main(){
Node* root = NULL;
//it will create a node
root = newnode(34);
root->left = newnode(12);
root->right = newnode(50);
root->left->left = newnode(11);
root->left->right = newnode(54);
levels(root);
return 0;
}输出
如果我们运行上述程序，它将生成以下输出
Level of 34 is 1 Level of 12 is 2 Level of 50 is 2 Level of 11 is 3 Level of 54 is 3
更新于: 2019-09-04
203 次浏览
广告