数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在 C++ 编程中打印二叉树中任意两个节点之间的路径。
我们给定一个具有不同节点的二叉树，以及二叉树的两个节点，我们希望打印这两个节点在二叉树中的路径。
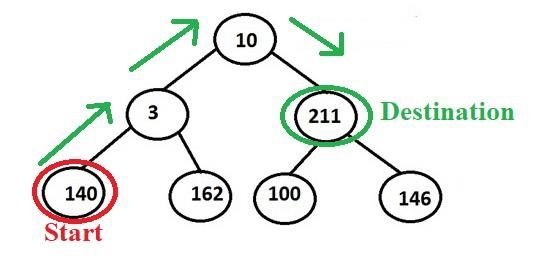
例如 - 我们希望打印从节点 140 到 211 的路径，因此其输出应类似于 -
Output: 140->3->10->211
这个想法是从根节点找到到这两个节点的路径，并将它们存储在两个单独的向量或数组中，例如 path1 和 path2。
现在，出现了两种不同的情况 -
- 如果两个节点位于根节点的不同子树中 - 当两个节点位于不同的子树中，例如一个在左边，另一个在右边。在这种情况下，很明显，根节点将位于从节点 1 到节点 2 的路径之间。因此，以相反的顺序打印 path1，然后打印 path2。
如果节点位于同一子树中 - 当两个节点都位于同一子树中时，这可以是左子树或右子树。在这种情况下，您需要观察从根节点到这两个节点的路径将在某个交点之前是两个节点从根节点的公共路径。我们必须找到交点并像上面那样打印从该点开始的节点。
算法
START STEP 1-> DEFINE A struct Node WITH int data AND Node *left, *right; STEP 2-> DEFINE A TREE STRUCTURE struct Node* tree(int data)FUNCTION bool path(Node* root, vector& arr, int x) STEP 1-> IF root IS NULL RETURN false END IF STEP 2-> arr.push_back(root->data) IF root->data == x THEN RETURN true END IF STEP 3-> IF path(root->left, arr, x) || path(root->right, arr, x) THEN, RETURN true STEP 4-> arr.pop_back() return false END FUNCTION FUNCTION void printPath(Node* root, int n1, int n2) STEP 1-> DEFINE A vector<int> path1 STEP 2-> DEFINE A vector<int> path2 STEP 3-> CALL FUNCTION path(root, path1, n1) STEP 4-> CALL FUNCTION path(root, path2, n2) STEP 5-> DEFINE AND SET intersection = -1, i = 0, j = 0 STEP 6-> LOOP WHILE i != path1.size() || j != path2.size() IF i == j && path1[i] == path2[j] INCREMENT i BY 1 INCREMENT j BY 1 ELSE SET intersection = j - 1 BREAK; END IF END WHILE STEP 7-> LOOP FOR i = path1.size() – 1 AND i > intersection AND i--PRINT path1[i] END FOR STEP 8-> LOOP FOR i = intersection AND i < path2.size() AND i++ PRINT path2[i] END FOR
示例
#include <bits/stdc++.h>
using namespace std;
// structure of a node of binary tree
struct Node {
int data;
Node *left, *right;
};
struct Node* tree(int data){
struct Node* newNode = new Node;
newNode->data = data;
newNode->left = newNode->right = NULL;
return newNode;
}
bool path(Node* root, vector<int>& arr, int x){
if (!root)
return false;
// push the node's value in 'arr'
arr.push_back(root->data);
// if it is the required node
// return true
if (root->data == x)
return true;
if (path(root->left, arr, x) || path(root->right, arr, x))
return true;
arr.pop_back();
return false;
}
// Function to print the path between
// any two nodes in a binary tree
void printPath(Node* root, int n1, int n2){
// vector to store the path
vector<int> path1;
vector<int> path2;
path(root, path1, n1);
path(root, path2, n2);
int intersection = -1;
int i = 0, j = 0;
while (i != path1.size() || j != path2.size()) {
if (i == j && path1[i] == path2[j]) {
i++;
j++;
} else {
intersection = j - 1;
break;
}
}
// Print the required path
for (int i = path1.size() - 1; i > intersection; i--)
cout << path1[i] << " ";
for (int i = intersection; i < path2.size(); i++)
cout << path2[i] << " ";
}
int main(){
// binary tree formation
struct Node* root = tree(1);
root->left = tree(2);
root->left->left = tree(4);
root->left->left->left = tree(6);
root->left->right = tree(5);
root->left->right->left = tree(7);
root->left->right->right = tree(8);
root->right = tree(3);
root->right->left = tree(9);
root->right->right = tree(10);
int node1 = 5;
int node2 = 9;
printPath(root, node1, node2);
return 0;
}输出
此程序将打印输出 -
5 2 1 3 9
更新于: 2019-09-04
389 次浏览
广告