使用 C++ 在 BST 中查找第二大元素

在二叉搜索树 (BST) 中，必须返回第二大元素。在二叉树中，第二大元素是最大的元素。


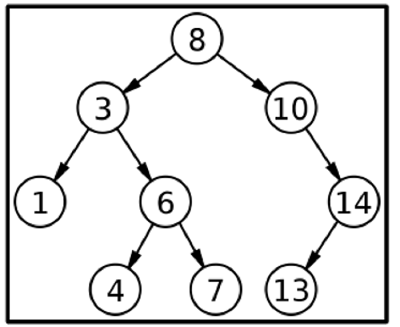
根据给定的 BST，13 是第二大元素。现在我们使用 C++ 方法来解决这个问题。我们可以遍历树的中序遍历，通过观察，我们可以观察到给定 BST 中的第二大元素是 13。树的中序遍历将是 1 3 4 6 7 8 10 13 14，我们可以观察到元素位于排序数组中。因此，我们返回第二大元素。

让我们假设一些简单的输入和输出场景

假设二叉树中的元素如下所示。这里二叉搜索树中只有两个元素。通过比较节点的值，第二大的值为6。

Input = BST
     11
     /
    6
Output = Second largest element in BST will be: 6

还可以考虑以下场景，因为下面有一个二叉搜索树，并且具有大量的节点。下面二叉树的输出将是

Input = BST
       11
      /  \
     6   21
    /     \
   4       31
Output = Second largest element in BST will be: 21

算法

以下步骤是解决问题的方法。

  • 实现二叉搜索树 (BST)。

  • 将节点的值插入 BST。

  • 使用中序遍历技术，左 -> 根 -> 右 (L-R-R)

  • 然后使用[inorder.size()-2];在 BST 中找出第二大的节点值。

示例

以下是查找二叉搜索树中第二大元素的 C++ 代码：

#include <iostream>
#include <vector>
using namespace std;
class Node {
   public:
   int val;
   Node *left, *right;
   Node(int val) {
      this->val = val;
      left = right = NULL;
   }
};
void solve(Node* root, vector<int>& inorder) {
   if(root == NULL) return;
      solve(root->left, inorder);
   inorder.push_back(root->val);
   solve(root->right, inorder);
}
int main() {
   Node* root = new Node(8);
   root->left = new Node(3);
   root->right = new Node(10);
   root->left->left = new Node(1);
   root->left->right = new Node(6);
   root->left->right->left = new Node(4);
   root->left->right->right = new Node(7);
   root->right->right = new Node(14);
   root->right->right->left = new Node(13);
   vector<int> inorder;
   solve(root, inorder);
   cout << "Second largest element of this BST is : " << inorder[inorder.size()- 2];
   return 0;
}

输出

Second largest element of this BST is: 13

结论

这是一个纯粹基于观察的问题，我们需要观察树的中序遍历的模式。此算法的时间复杂度为中序遍历的 O(n)。

更新于： 2022 年 8 月 10 日

630 次查看

开启您的 职业生涯

通过完成课程获得认证

开始
广告