数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会学
时尚
法律C++ 中两个 BST 节点之间的最大元素
问题陈述
给定一个 N 元素数组和两个整数 A、B，它们属于给定数组。通过从 arr[0] 到 arr[n-1] 插入元素来创建一个二叉搜索树。任务是从 A 到 B 的路径中找到最大元素。
示例
如果数组为 {24, 23, 15, 36, 19, 41, 25, 35}，我们可以形成如下所示的 BST −
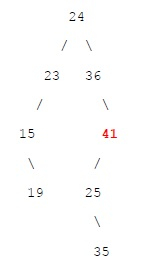
如果我们考虑 A = 19 且 B = 41，则这两个节点之间的最大元素为 41
算法
- 找到节点 A 和 B 的最低公共祖先 (LCA)。
- 在 LCA 和 A 之间找到最大节点。我们称之为 max1
- 在 LCA 和 B 之间找到最大节点。我们称之为 max2
- 返回 max1 和 max2 的最大值
示例
现在让我们看一个示例 −
#include <bits/stdc++.h>
using namespace std;
struct node {
int data;
struct node* left;
struct node* right;
};
node *createNode(int x) {
node *p = new node();
p -> data = x;
p -> left = NULL;
p -> right = NULL;
return p;
}
void insertNode(struct node *root, int x) {
node *p = root, *q = NULL;
while (p != NULL) {
q = p;
if (p -> data < x) {
p = p -> right;
} else {
p = p -> left;
}
}
if (q == NULL) {
p = createNode(x);
} else {
if (q -> data < x) {
q -> right = createNode(x); } else {
q -> left = createNode(x);
}
}
}
int maxelpath(node *q, int x) {
node *p = q;
int mx = INT_MIN;
while (p -> data != x) {
if (p -> data > x) {
mx = max(mx, p -> data);
p = p -> left;
} else {
mx = max(mx, p -> data);
p = p -> right;
}
}
return max(mx, x);
}
int getMaximumElement(struct node *root, int x, int y) {
node *p = root;
while ((x < p -> data && y < p -> data) || (x > p ->
data && y > p -> data)) {
if (x < p -> data && y < p -> data) {
p = p -> left;
} else if (x > p -> data && y > p -> data) {
p = p -> right;
}
}
return max(maxelpath(p, x), maxelpath(p, y));
}
int main() {
int arr[] = {24, 23, 15, 36, 19, 41, 25, 35}; int a = 19, b = 41;
int n = sizeof(arr) / sizeof(arr[0]);
struct node *root = createNode(arr[0]);
for (int i = 1; i < n; i++) insertNode(root, arr[i]);
cout << "Maximum element = " << getMaximumElement(root, a, b) << endl;
return 0;
}输出
Maximum element = 41
更新日期： 2019 年 12 月 31 日
198 次浏览
广告