C++程序查找二叉搜索树中两个节点之间的最短距离

在这篇文章中，我们给定一个BST（二叉搜索树），我们需要找到BST中两个给定节点之间的最短距离。让我们来看一个树，以下是几种情况。

让我们假设一些简单的输入和输出场景


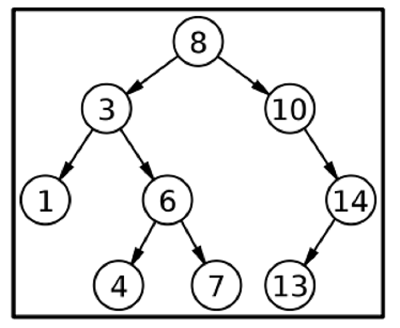
现在我们必须找到节点4和13之间的距离。

int key1=13, key2=4;
res = solve(root, min(key1,key2), max(key1,key2));
output = 6

最短距离是6，路径是4->6->3->8->10->14->13（箭头表示路径定义，仅此而已）。

让我们在上面的图中找到来自两个不同节点的另一个距离。考虑从节点7到节点14的距离。(6->3->8->10->14)，同样，这里的箭头定义了路径。这里最短距离是5。

Int key1=7, key2=14;
res = solve(root, min(key1,key2), max(key1,key2));
output = 5

因此，BST中最短的距离肯定包含LCA（最近公共祖先）。所以在给定的例子中，LCA是8。所以我们可以找到节点4与8的距离，节点13与8的距离，然后将它们加起来。所以在这个问题中，我们必须找到给定两个节点的LCA。现在，为了在BST中找到LCA，我们可以检查以下条件：

  • 如果两个值都小于根，则LCA在左侧

  • 如果两个值都大于根，则LCA在右侧

  • 如果一个值小于根，另一个值大于根，则该节点是LCA

算法

在二叉搜索树的情况下，查找距离比其他树快一些。以下是执行所需任务的算法/步骤：

  • 步骤1 - 以二叉搜索树和两个节点作为输入，推导出一个方法来查找这两个节点之间的距离。

  • 步骤2 - 在三种情况下计算距离

    • 如果一个节点在左子树中，另一个节点在右子树中，则计算左侧节点的深度（从根到该节点的距离），并将其添加到右侧节点的深度。

    • 如果两个节点都在左子树中，则将根的左孩子作为新的根，并计算左节点的深度，然后将其添加到右节点相对于新根的深度。递归地找到根，直到一个节点在左子树中，另一个节点在右子树中。

    • 同样，如果两个节点都在右子树中，则递归地将根的右孩子作为新的根，并计算左节点的深度，然后将其添加到右节点相对于新根的深度。

  • 步骤3 - 得到的结果将是这两个节点之间的距离。

示例

下面的C++实现查找二叉搜索树中两个节点之间的最短距离：

Open Compiler
#include <iostream>
using namespace std;
class Node {
   public:
   int val;
   Node *left, *right;
   Node(int val) {
      this->val = val;
      left = right = NULL;
   }
};
int distance(Node* root, int val) {
   if(root->val == val) return 0;
      else if(root->val > val) return 1+distance(root->left, val);
   else return 1+distance(root->right, val);
}
int solve(Node* root, int key1, int key2) {
   if(root->val > key1 && root->val < key2) {
      return distance(root, key1) + distance(root, key2);
   } else if(root->val > key1 && root->val > key2) {
      return solve(root->left, key1, key2);
   } else {
      return solve(root->right, key1, key2);
   }
}
int main() {
   Node* root = new Node(8);
   root->left = new Node(3);
   root->right = new Node(10);
   root->left->left = new Node(1);
   root->left->right = new Node(6);
   root->right->right = new Node(14);
   root->left->right->left = new Node(4);
   root->left->right->right = new Node(7);
   root->right->right->left = new Node(13);
   int key1=13, key2=4;
   cout << solve(root, min(key1,key2), max(key1,key2));
   return 0;
}

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

输出

6

结论

代码假设输入正确，并且key1和key2有效。对于无效输入，我们可以使root等于NULL并显示自定义消息。算法的时间复杂度为O(h)，其中h是树的高度。

更新于：2022年8月10日

727 次查看

启动你的职业生涯

完成课程获得认证

开始学习
广告