数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究使用弗洛伊德·沃歇尔算法查找任意两个节点之间的最短路径
C++ 有一种宏，它被定义为一段代码或期望值，并且会在用户需要时重复使用。弗洛伊德·沃歇尔算法是在给定的加权图中找到所有顶点对之间最短路径的过程。该算法遵循动态规划方法来找到最小权重图。
让我们借助图表了解什么是弗洛伊德·沃歇尔算法 -
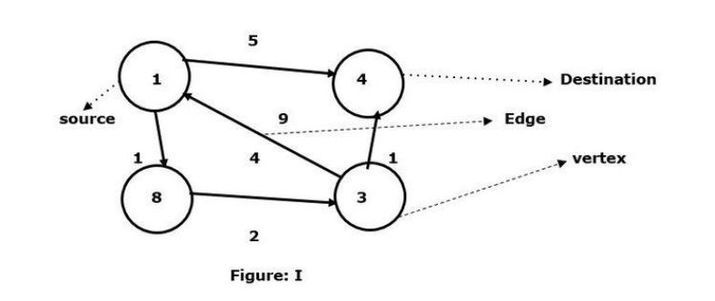
将顶点1作为源顶点，将顶点4作为目标顶点，并找到它们之间的最短路径。
我们已经看到有两条路径可以连接到目标顶点 4。
1 -> 4 – 边权重为 5
1 -> 8 -> 3 -> 4 – 边权重 (1+2+1) 为 4。
在图 I 中，我们看到两个顶点之间连接的最小边。因此，这里顶点8和顶点3连接了顶点1到顶点4的路径，边的最小权重为4。另一方面，顶点1到顶点4之间有一条有向边，边的权重为5。
现在我们比较这两个权重，即4和5。因此，这里4是弗洛伊德·沃歇尔算法意义上的图的最小权重。
在本文中，我们将使用弗洛伊德·沃歇尔算法解决任意两个给定节点之间的最短路径问题。
语法
程序中使用以下语法 -
data_type[][] array_name;
参数
data_type[][] - 用户提到的数据类型。第一个数组表示行，第二个数组表示列。因此，这表示二维数组。
array_name - 给数组起的名字。
算法
我们将从名为'iostream'的头文件开始程序，并将宏位置定义为'INF'（无穷大），因为稍后它将遇到 2D 数组矩阵和 if-else 语句。
接下来，我们创建名为'printPath'的全局函数定义，并接受三个参数，即'parent[]'、'i'和'j'，以验证路径是否存在。
然后我们开始主函数，并将值'4'存储到变量'V'中，它表示顶点数。其次，将值以邻接矩阵的形式存储到'dist[V][V]'变量中。众所周知，dist[i][j]表示定义从'i'到'j'的边权重的二维矩阵，通过存储邻接矩阵来实现。
接下来，我们为'parent'变量初始化二维数组，并具有大小[V][V]。
在此变量中，我们用于显示每对顶点'i'和'j'相对于'parent[i][j]'。
通过使用两个嵌套的 for 循环，我们将找到最短路径。第一个 for 循环迭代矩阵中的行。继续使用第二个 for 循环，它迭代矩阵中的列，然后我们将使用 if-else 语句检查以下条件 -
if (dist[i][j] != INF && i != j){ parent[i][j] = i;}
在 if 语句中，我们使用'and' (&&)运算符来显示两个条件，如果这两个条件都满足，则'i'将存储到'parent[i][j]'中，这验证了路径的存在。
else { parent[i][j] = -1;}
在 else 语句中，我们将'-1'初始化为'parent[i][j]'，这验证了路径不存在。
现在我们从三个嵌套的for循环开始，并在 0 到 V-1 的范围内应用 k 顶点，借助此范围，我们的最短距离和路径将更新。在第三个嵌套循环内，我们使用以下条件，例如
if (dist[i][j] < dist[i][k] + dist[k][j]){
dist[i][j] = dist[i][k] + dist[k][j];
parent[i][j] = parent[k][j];
}
接下来，我们通过给出以下条件，打印所有顶点对的最短距离和路径，例如
通过使用两个嵌套的 for 循环，我们打印最短距离和路径。
通过在第二个 for 循环下使用 if 语句，我们将检查 dist[i][j] 是否等于无穷大。如果发现它为无穷大，则它将打印'INF'，否则它将打印最短路径。
最后，我们调用名为'printPath()'的函数以通过传递三个参数（即 parent[i]、i 和 j）来获取最短路径的值。
这里 K 正在更新二维数组矩阵中行和列的一部分，这验证了新更新的最短路径和距离。
示例
在此程序中，我们将使用弗洛伊德·沃歇尔算法计算任意两个节点之间的最短路径。
#include <iostream>
using namespace std;
#define INF 1000000000 // Infinity
void printPath(int parent[], int i, int j) {
if (i == j)
cout << i << " ";
else if (parent[j] == -1)
cout << "No path exists";
else
{
printPath(parent, i, parent[j]);
cout << j << " ";
}
}
int main()
{
int V = 4;
// V represent number of vertices
int dist[V][V] = {{0, 2, INF, 4},
{6, 0, 5, 3},
{INF, 10, 0, 1},
{7, 9, 8, 0}};
// Represent the graph using adjacency matrix
// Apply the Floyd Warshall algorithm to find the shortest paths
int parent[V][V];
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (dist[i][j] != INF && i != j)
parent[i][j] = i;
else
parent[i][j] = -1;
}
}
// update the path and distance using the k vertex range from 0 to V-1.
for (int k = 0; k < V; k++)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (dist[i][j] > dist[i][k] + dist[k][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
parent[i][j] = parent[k][j];
}
}
}
}
// Print shortest distances and paths between all pairs of vertices
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
cout << "The Shortest distance between " << i << " and " << j << " is ";
if (dist[i][j] == INF)
cout << "INF ";
else
cout << dist[i][j] << " ";
cout << "and the shortest path is:- ";
printPath(parent[i], i, j);
cout << endl;
}
}
return 0;
}
输出
The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3
结论
我们学习了使用弗洛伊德·沃歇尔算法查找任意两个节点之间最短路径的概念。我们使用邻接矩阵作为程序的输入，在其中找到最短路径和距离。除此之外，为了更新路径和距离，我们使用 k 顶点来更新行和列。在我们的日常生活中，我们在 Google 地图上搜索从一个源到目的地的最短路线或路径。
952 次查看
