数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究二叉树中两个节点之间距离查询 - C++ 中 O(logn) 方法
在这个问题中，我们给定一棵二叉树和 Q 个查询。我们的任务是创建一个程序来解决二叉树中两个节点之间距离查询 - C++ 中 O(logn) 方法。
问题描述
在每个查询中，我们给定二叉树的两个节点，我们需要找到这两个节点之间的距离，即从一个节点到达另一个节点需要遍历的边数。
让我们举个例子来理解这个问题，
输入：二叉树
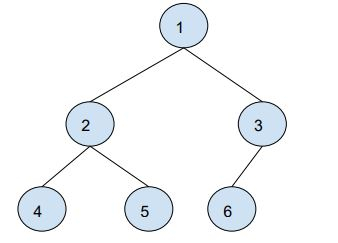
查询 = 3
Q1 -> [2, 6]
Q2 -> [4, 1]
Q3 -> [5, 3]
输出3, 2, 3
解决方案方法
为了解决这个问题，我们将使用距离公式，该公式使用最低公共祖先 (LCA) 及其距离。
Distance(n1, n2) = distance(root,n1) + distance(root,n1) - 2 * distance(root,LCA)
为了解决这个问题，我们将遵循以下步骤，
找到每个节点的层级，即 N1、N2、LCA。
然后，我们将根据树的欧拉遍历创建二叉树的数组。
然后，我们将为 LCA 创建一个线段树。
示例
#include <bits/stdc++.h>
#define MAX 1000
using namespace std;
int eulerArray[MAX];
int eIndex = 0;
int vis[MAX];
int L[MAX];
int H[MAX];
int level[MAX];
struct Node {
int data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int data) {
struct Node* temp = new struct Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void FindNodeLevels(struct Node* root) {
if (!root)
return;
queue<pair<struct Node*, int> > q;
q.push({ root, 0 });
pair<struct Node*, int> p;
while (!q.empty()) {
p = q.front();
q.pop();
level[p.first->data] = p.second;
if (p.first->left)
q.push({ p.first->left, p.second + 1 });
if (p.first->right)
q.push({ p.first->right, p.second + 1 });
}
}
void createEulerTree(struct Node* root) {
eulerArray[++eIndex] = root->data;
if (root->left) {
createEulerTree(root->left);
eulerArray[++eIndex] = root->data;
}
if (root->right) {
createEulerTree(root->right);
eulerArray[++eIndex] = root->data;
}
}
void creareEulerArray(int size) {
for (int i = 1; i <= size; i++) {
L[i] = level[eulerArray[i]];
if (vis[eulerArray[i]] == 0) {
H[eulerArray[i]] = i;
vis[eulerArray[i]] = 1;
}
}
}
pair<int, int> seg[4 * MAX];
pair<int, int> min(pair<int, int> a, pair<int, int> b) {
if (a.first <= b.first)
return a;
else
return b;
}
pair<int, int> buildSegTree(int low, int high, int pos) {
if (low == high) {
seg[pos].first = L[low];
seg[pos].second = low;
return seg[pos];
}
int mid = low + (high - low) / 2;
buildSegTree(low, mid, 2 * pos);
buildSegTree(mid + 1, high, 2 * pos + 1);
seg[pos] = min(seg[2 * pos], seg[2 * pos + 1]);
}
pair<int, int> LCA(int qlow, int qhigh, int low, int high, int pos) {
if (qlow <= low && qhigh >= high)
return seg[pos];
if (qlow > high || qhigh < low)
return { INT_MAX, 0 };
int mid = low + (high - low) / 2;
return min(LCA(qlow, qhigh, low, mid, 2 * pos), LCA(qlow, qhigh,mid + 1, high, 2 * pos +1));
}
int CalcNodeDistance(int node1, int node2, int size) {
int prevn1 = node1, prevn2 = node2;
node1 = H[node1];
node2 = H[node2];
if (node2 < node1)
swap(node1, node2);
int lca = LCA(node1, node2, 1, size, 1).second;
lca = eulerArray[lca];
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
int main() {
int N = 6;
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
FindNodeLevels(root);
createEulerTree(root);
creareEulerArray(2 * N - 1);
buildSegTree(1, 2 * N - 1, 1);
int Q = 4;
int query[Q][2] = {{1, 5}, {4, 6}, {3, 4}, {2, 4} };
for(int i = 0; i < Q; i++)
cout<<"The distance between two nodes of binary tree is "<<CalcNodeDistance(query[i][0], query[i][1], 2 * N - 1)<<endl;
return 0;
}输出
The distance between two nodes of binary tree is 2 The distance between two nodes of binary tree is 4 The distance between two nodes of binary tree is 3 The distance between two nodes of binary tree is 1
更新于： 2020-10-09
117 次查看
广告