Python程序：计算具有n个节点的BST数量

假设我们有n个不同的节点，所有节点都不同。我们必须找到有多少种方法可以将它们排列成二叉搜索树。众所周知，对于二叉搜索树，左子树总是保存较小的值，而右子树保存较大的值。

为了解决这个问题，我们将找到卡特兰数。卡特兰数C(n)表示具有n个不同键的二叉搜索树。公式如下：

$$C(n)=\frac{(2n)!}{(n+1)!\times n!}$$

因此，如果输入为n = 3，则输出为5，因为……

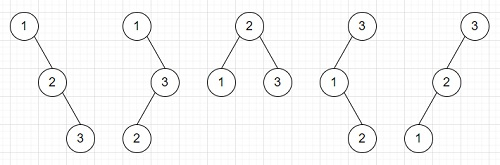
为了解决这个问题，我们将遵循以下步骤：

  • 定义一个函数ncr()。这将需要n, r。
  • res := 1
  • 如果r > n - r，则
    • r := n - r
  • 对于i in range 0 to r - 1，执行：
    • res := res *(n - i)
    • res := floor of (res/(i + 1))
  • 返回res
  • 从主方法中执行以下操作：
  • c := ncr(2 * n, n)
  • 返回floor of c /(n + 1)

示例

让我们来看下面的实现以更好地理解：

from math import factorial

def ncr(n, r):
   res = 1
   if r > n - r:
      r = n - r

   for i in range(r):
      res *= (n - i)
      res //= (i + 1)

   return res

def solve(n):
   c = ncr(2 * n, n)
   return c // (n + 1)

n = 3
print(solve(n))

输入

3

输出

5

更新于：2021年10月12日

246 次浏览

开启您的职业生涯

完成课程获得认证

开始学习
广告