电力站如何在需求增加时产生更多的千瓦 (kW) 输出？

发电站的有用输出是千瓦 (kW) 输出，该输出由发电站输送到电力供应系统。有时，发电站需要提供更多千瓦以满足增加的电力需求。这可以通过以下两种方法中的任何一种实现：

• 提高视在功率 (kVA) 容量 – 在此方法中，发电站的视在功率容量在相同的功率因数下增加，以满足增加的千瓦需求。尽管如此，增加发电站的视在功率容量会导致额外的成本。

• 提高功率因数 – 在此方法中，发电站的功率因数得到改善，例如从 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 提高到 $\mathrm{cos}\, \phi _{\mathrm{2}}$，而无需增加发电站的视在功率容量来满足增加的千瓦需求。它还会因功率因数校正设备而导致额外的成本。

两种方法的经济比较

从满足发电站增加的千瓦需求的两种方法的定义可以看出，每种方法都涉及额外成本。因此，我们需要对这两种方法进行经济比较。

考虑一个额定为 S kVA 的发电站，以功率因数 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 向负载供电。众所周知，增加的电力需求可以通过以下两种方式之一来满足：将功率因数从 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 提高到 $\mathrm{cos}\, \phi _{\mathrm{2}}$，保持 S kVA 不变；或者在原始功率因数 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 下提高发电站的 kVA 额定值。

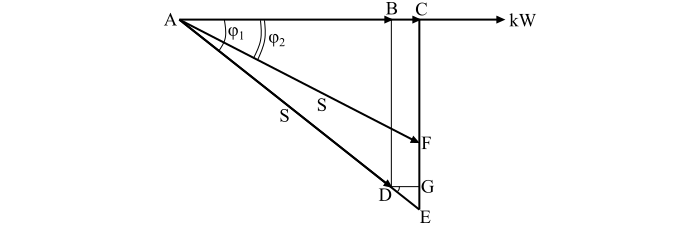
提高发电站 kVA 容量的成本

参考图中所示的功率三角形。为了满足增加的千瓦需求，在原始功率因数 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 下增加的发电站的视在功率容量由下式给出：

$$\mathrm{增加的视在功率容量\: \mathit{\mathrm{\, =\, }DE\mathrm{\, =\, }\frac{DG}{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }\frac{BC}{\mathrm{cos}\, \phi _{\mathrm{1}}};\; \; \; \left ( \because DG\mathrm{\, =\, }BC \right )}}$$

$$\mathrm{\Rightarrow 增加的视在功率容量\mathit{\mathrm{\, =\, }\frac{AC-AB}{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }\frac{AF\,\mathrm{cos}\, \phi _{\mathrm{2}}-AD\,\mathrm{cos}\, \phi _{\mathrm{1}} }{\mathrm{cos}\, \phi _{\mathrm{1}}}}}$$

$$\mathrm{\Rightarrow 增加的视在功率容量 \mathit{\mathrm{\, =\, }\frac{S\left ( \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{cos}\, \phi _{\mathrm{1}} \right )}{\mathrm{cos}\, \phi _{\mathrm{1}}};\; \; \left ( \because AF\mathrm{\, =\, }AD\mathrm{\, =\, }S \right )}}$$

现在，假设发电站每千伏安 (kVA) 每年的成本为 x 元，那么由于增加的视在功率容量而产生的每年成本为

$$\mathrm{由于增加的视在功率容量导致的年成本 \mathit{\mathrm{\, =\, }x元\left [ \frac{S\left ( \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{cos}\, \phi _{\mathrm{1}} \right )}{\mathrm{cos}\, \phi _{\mathrm{1}}} \right ] }}$$

功率因数校正设备的成本

可以通过将功率因数从 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 提高到 $\mathrm{cos}\, \phi _{\mathrm{2}}$，而无需增加发电站的视在功率容量来满足增加的千瓦需求。

参考上图中给出的功率三角形，功率因数校正设备需要提供的超前无功功率 (kVAR) 由下式给出：

$$\mathrm{超前无功功率 \mathit{\mathrm{\, =\, }FE\mathrm{\, =\, }CE-CF}}$$

$$\mathrm{\Rightarrow 超前无功功率 \mathit{\mathrm{\, =\, }AE\, \mathrm{sin}\, \phi _{\mathrm{1}}-AF\, \mathrm{sin}\, \phi _{\mathrm{2}}}}$$

$$\mathrm{\Rightarrow 超前无功功率 \mathit{\mathrm{\, =\, }\frac{AC}{\mathrm{cos}\, \phi _{\mathrm{1}}}\, \mathrm{sin}\, \phi _{\mathrm{1}}-AF\, \mathrm{sin}\, \phi _{\mathrm{2}}}}$$

$$\mathrm{\Rightarrow 超前无功功率\mathit{\mathrm{\, =\, }\frac{AF\, \mathrm{cos}\, \phi _{\mathrm{2}}}{\mathrm{cos}\, \phi _{\mathrm{1}}}\, \mathrm{sin}\, \phi _{\mathrm{1}}-AF\, \mathrm{sin}\, \phi _{\mathrm{2}}}}$$

$$\mathrm{\Rightarrow 超前无功功率 \mathit{\mathrm{\, =\, }AF\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$

$$\mathrm{\therefore 超前无功功率 \mathit{\mathrm{\, =\, }S\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$

现在，假设功率因数校正设备每千乏 (kVAR) 每年的成本为 y 元，那么功率因数校正设备的年成本为

$$\mathrm{功率因数校正设备的成本\mathit{\, \mathrm{\, =\, }\, y元\, S\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$

数值示例

一个发电站以其最大视在功率容量工作，功率因数为 0.75 滞后。现在需要增加其千瓦容量以满足增加的负载需求。这可以通过以下方式实现：

• 安装一个额外的发电站，成本为每千伏安 850 元，或者

• 通过安装功率因数校正设备将功率因数提高到 0.85 滞后。

为了使功率因数校正设备的使用比增加发电站更经济，功率因数校正设备的最大成本（每千伏安）是多少？

解决方案

假设发电站的初始视在功率容量为 S kVA，功率因数为 $\mathrm{cos}\, \phi _{\mathrm{1}}$。

• 提高视在功率容量的成本 –

  $$\mathrm{提高视在功率容量的成本 \mathit{\mathrm{\, =\, }850元\times \left [ \frac{\mathit{S}\left ( 0.85-0.75 \right )}{0.75} \right ]}}$$

  $$\mathrm{提高视在功率容量的成本 \mathit{\mathrm{\, =\, }113.33元\times \mathit{S}\; \; \cdot \cdot \cdot \left ( 1 \right )}$$

• 功率因数校正设备的成本 –

功率因数角 $\mathrm{\phi _{1}}$ 和 $\mathrm{\phi _{2}}$ 由下式给出：

$$\mathrm{\phi _{1}\, =\, cos^{-1}\, 0.75\, =\,41.41^{\circ }\: 和\: \phi _{2}\, =\, cos^{-1}\, 0.85\, =\,31.78^{\circ }}$$

$$\mathrm{\therefore 功率因数校正设备的成本\mathit{\, \mathrm{\, =\, }\, y元\, S\left ( \mathrm{tan}\, \phi _{\mathrm{1}}\, \mathrm{cos}\, \phi _{\mathrm{2}}-\mathrm{sin}\, \phi _{\mathrm{2}} \right )}}$$

$$\mathrm{\Rightarrow 功率因数校正设备的成本\mathit{\, \mathrm{\, =\, }\, y元\,\times S\times \left ( \mathrm{tan\, 41.41^{\circ }\times 0.85}-\mathrm{sin\, 31.78^{\circ }}\, \right )}}$$

$$\mathrm{\therefore 功率因数校正设备的成本\mathit{\, \mathrm{\, =\, }\, 0.223元\times y\times S\; \; \; \cdot \cdot \cdot }\left ( 2 \right )}$$

当公式 (1) 和 (2) 相等时，即证明了功率因数校正设备每千伏安的成本能够证明其安装的合理性，即

$$\mathrm{113.33 \times \mathit{S}\, \mathrm{\, =\, }\, 0.223 \times \mathit{y} \times \mathit{S}}$$

$$\mathrm{\mathit{\Rightarrow y}\mathrm{\, =\, }\frac{113.33}{0.223}\mathrm{\, =\, }508.2元/千乏}$$

当功率因数校正设备为理想状态时，其千乏 (kVAR) 等于千伏安 (kVA)。因此，功率因数校正设备的最大成本（每千伏安）为 508.2 元。

Manish Kumar Saini

更新于： 2022 年 2 月 10 日

422 次浏览

开启你的职业生涯

完成课程获得认证

开始学习