如何将有限自动机转换为正则表达式？

问题

将给定的有限自动机 (FA) 转换为正则表达式 (RE)。

解答

将DFA转换为正则表达式有两种常用的方法：

  • Arden 方法
  • 状态消除法

让我们考虑使用状态消除法将 FA 转换为 RE。

规则

状态消除法的规则如下：

规则 1

DFA 的初始状态不能有任何入边。

如果初始状态有任何入边，则创建一个新的初始状态，使其没有任何入边。

规则 2

DFA 中必须只有一个最终状态。

如果存在多个最终状态，则将所有最终状态转换为非最终状态，并创建一个新的单个最终状态。

规则 3

DFA 的最终状态不能有任何出边。

如果存在，则创建一个新的最终状态，使其没有任何出边。

规则 4

逐一消除所有中间状态。

现在，应用这些规则可以轻松地将 FA 转换为 RE。

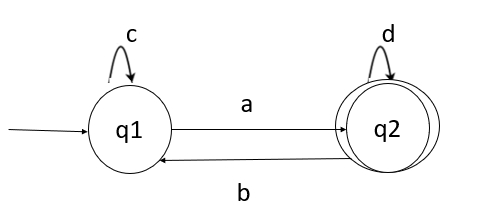
给定的 FA 如下：

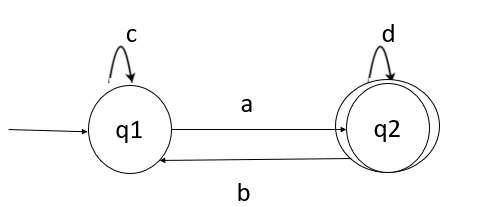
步骤 1

初始状态 q1 有一个入边，因此创建一个新的初始状态 qi。

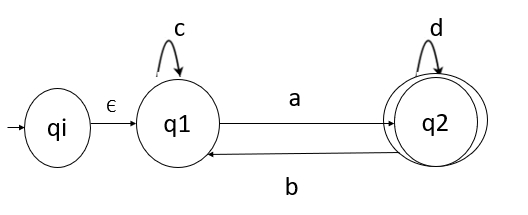
步骤 2

最终状态 q2 有一个出边。因此，创建一个新的最终状态 qf。

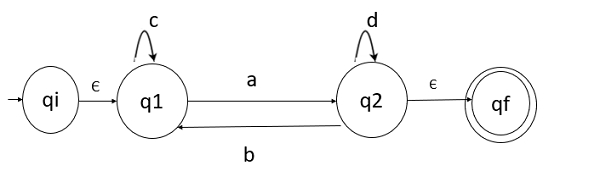
步骤 3

开始消除中间状态

首先消除 q1

有一条路径通过 q1 从 qi 到 q2。因此，在消除 q1 后，我们可以连接从 qi 到 q2 的直接路径，其代价为：

εc*a=c*a

使用状态 qi 在 q2 上有一个循环。因此，在消除 q1 后，我们向 q2 添加一个直接循环，其代价为：

b.c*.a=bc*a

消除 q1 后，FA 看起来像这样：

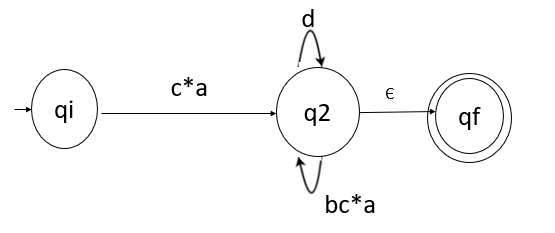
其次消除 q2

有一条从 qi 到 qf 的直接路径，因此，我们可以直接消除 q2，其代价为：

C*a(d+bc*a)* ε = c*a(d+bc*a)*

这就是给定有限自动机的最终正则表达式。

更新于：2021年6月12日

9000+ 次浏览

开启您的职业生涯

完成课程获得认证

开始学习
广告