数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
服装研究
法律研究如何在计算理论 (TOC) 中使用图灵机识别语言？
图灵机 (TM) 可以正式描述为七元组：
(Q,X, ∑, δ,q0,B,F)
其中：
Q 是有限状态集。
X 是带字母表。
∑ 是输入字母表。
δ 是转移函数：𝛿:QxX->QxXx{左移，右移}。
q0 是初始状态。
B 是空白符号。
F 是最终状态。
当且仅当图灵机 T 从初始位置开始，x 写在磁带上，并且 T 停留在最终状态时，图灵机 T 识别字符串 x（在 ∑ 上）。
T 停留在最终状态。
如果 x 被 T 识别，当且仅当 x 属于 A 时，则称 T 识别语言 A。
请注意，在运行 TM 时，您还可以读取/写入磁带上的其他符号，而不必仅限于字母表 A 中的符号。
如果图灵机 T 没有停留在非最终状态，则它不识别字符串 x。
有些 TM 对于某个输入根本不会停止，而是一直运行。
瞬时描述
要描述给定时间的 TM，我们需要了解以下三点：
磁带上有什么？
磁头在哪里？
控制处于什么状态？
我们将用以下方式表示此信息：
状态 i − B a a b a b B
这里，B 符号表示空单元格（无限重复到左边和右边），磁头的位置以红色显示。
示例
对于 ∑ = {a, b}，设计一个接受由正则表达式 a* 表示的语言的图灵机。
步骤 1 - 从输入的左端开始，我们读取每个符号并检查它是否是 a。
步骤 2 - 如果是，我们继续向右移动。
步骤 3 - 如果我们在遇到除 a 之外的任何符号之前到达空白符号，我们终止并接受该字符串。
步骤 4 - 如果输入在任何地方包含 b（字符串不在 L(a*) 中），我们会在非最终状态下停止。
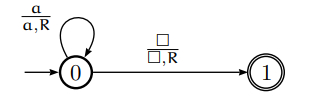
为了跟踪计算，两个状态 0（初始）和 1（最终）就足够了。作为转移函数，我们可以使用：
T(0, a) = (0, a, R),
T(0,B ) = (1,B , R)
或者我们可以画一个图：
更新于：2021年6月16日
969 次浏览
广告