数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在计算理论中解释多磁带图灵机？
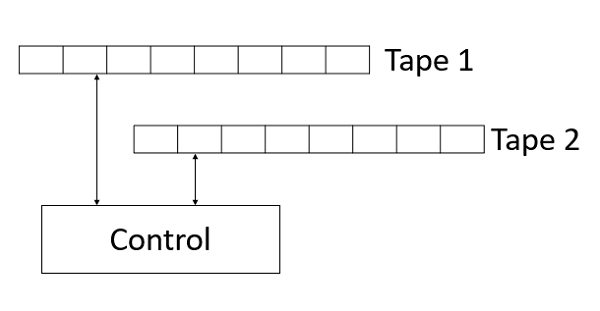
具有多个磁带的图灵机（TM）称为多磁带图灵机。
每个磁带都有自己的读/写磁头。
对于 N 磁带图灵机
M={( Q,X, ∑,δ,q0,B,F)}
我们将多磁带图灵机定义为具有 k 个磁带和 k 个磁头独立移动的机器（多轨迹图灵机的推广）。
δ=QxXN ->Q x XN x {L,R}N
每个 TM 都有自己的读写磁头，但状态对所有磁头都是共有的。多磁带 TM 如下所示：
在每个步骤（转换）中，TM 读取所有磁头扫描的符号，根据这些符号和当前状态，每个磁头写入、向右或向左移动，以及控制单元进入新状态。
磁头的动作彼此独立。
示例
将两个数字（每个数字都表示为一个一元字符串）相乘以得到第三个数字，这对于简单的图灵机来说很难做到，但对于三磁带机器来说却相当简单。
计算开始前的磁带 计算开始前第二次加法的磁带
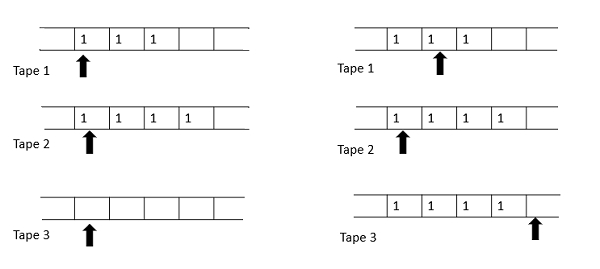
首先检查这两个数字是否为零：
(0,(B,B ,B ),(B,B ,B ),(S, S, S), Halt) 两者都为零
(0,(B, 1, B),(B, 1,B ),(S, S, S), Halt) 第一个为零
(0,(1,B ,B ),(1,B ,B ),(S, S, S), Halt) 第二个为零
(0,(1, 1, B),(1, 1B, ),(S, S, S), 1) 两者都不为零
将第二个磁带上的数字加到第三个磁带上：
(1,(1, 1,B ),(1, 1, 1),(S, R, R), 1) 复制
(1,(1,B ,B ),(1,B ,B ),(S, L, S), 2) 完成复制
将第二个磁带的磁头移动到数字的左端；将第一个数字的磁头向右移动一个单元格：
(2,(1, 1,B ),(1, 1,B ),(S, L, S), 2) 移动到左端
(2,(1,B ,B ),(1,B ,B ),(R, R, S), 3) 两种类型都向右移动一个单元格
检查第一个磁带磁头以查看是否已执行所有加法：
(3,(B, 1,B ),(B, 1,B ),(S, S, L), Halt) 完成
(3,(1, 1,B ),(1, 1,B ),(S, S, S), 1) 执行另一个加法
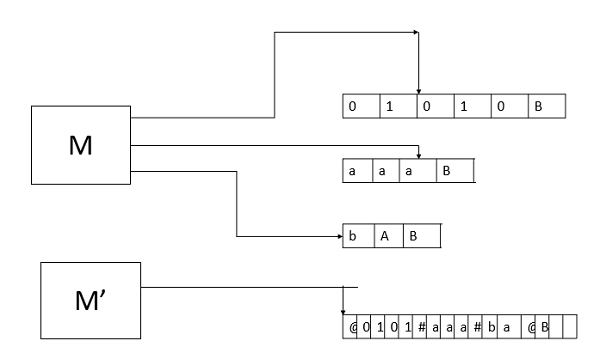
每个多磁带 TM 都有一个等效的单磁带 TM。
如果 M 有 k 个磁带，则 M0 通过在其单个磁带上存储相同的信息来模拟 k 个磁带的效果。
使用新的符号 # 作为分隔符来分隔不同磁带的内容（标记相关磁带部分的左/右端）。
M0 还必须跟踪每个磁带上磁头的位置。
在磁带符号上写一个带点的符号以标记该磁带上磁头所在的位置。带点符号只是添加到磁带字母表中的新符号。
如果一个 T 的磁带磁头的移动导致 M0 的磁头撞到 # 或 #，则必须移动磁带的该侧以腾出空间用于新的磁带单元格。
4K+ 次查看
