数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律学在美国和加拿大等国家，温度使用华氏度进行测量，而在印度等国家，则使用摄氏度进行测量。以下是一个将华氏度转换为摄氏度的线性方程
\[\mathrm{F}=\left(\frac{9}{5}\right) \mathrm{C}+32
\]
(i) 使用摄氏度作为x轴，华氏度作为\( y \)轴，绘制上述线性方程的图形。
(ii) 如果温度是\( 30^{\circ} \mathrm{C} \)，华氏度是多少？
(iii) 如果温度是\( 95^{\circ} \mathrm{F} \)，摄氏度是多少？
(iv) 如果温度是\( 0^{\circ} \mathrm{C} \)，华氏度是多少？如果温度是\( 0^{\circ} \mathrm{F} \)，摄氏度是多少？
(v) 是否存在一个温度在华氏度和摄氏度下数值相同？如果存在，请找出这个温度。
已知
将华氏度转换为摄氏度的线性方程为
$F=(\frac{9}{5})C+32$。
解题步骤
我们需要找到给定问题的解。
解答
已知：
$F=(\frac{9}{5})C+32$
(i) 以摄氏度为x轴，华氏度为y轴，在图上绘制线性方程。
我们知道：
要绘制一个二元线性方程的图形，我们需要至少两个解。
为了找到给定方程$F=(\frac{9}{5})C+32$的解。
让我们在方程$F=(\frac{9}{5})C+32$中代入$C=0$
对于$C=0$
我们得到：
$F=(\frac{9}{5})0+32$
$F=32$
对于$C=-10$
我们得到：
$F=(\frac{9}{5})(-10)+32$
$F=9(-2)+32$
$F=-18+32$
$F=14$
因此，
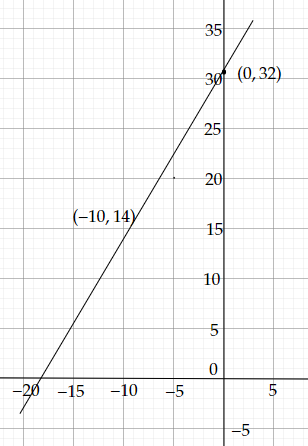
$(0, 32)$ 和 $(-10, 14)$ 是方程$F=(\frac{9}{5})C+32$的两个解。
因此，
二元线性方程$F=(\frac{9}{5})C+32$的图形是，(此处应插入图形)
(ii) 温度为$30^o\ C$，
这意味着：
$C=30$
将$C$代入线性方程$F=(\frac{9}{5})C+32$
我们得到：
$F=(\frac{9}{5})30+32$
$F=9(6)+32$
$F=54+32$
$F=86$
因此，华氏度温度为$86^o$。
(iii) 温度为$95^oF$
这意味着：
$F = 95$
将$F$代入线性方程$F=(\frac{9}{5})C+32$
我们得到：
$95=(\frac{9}{5})C+32$
$(\frac{9}{5})C=95-32$
$(\frac{9}{5})C=63$
$C=\frac{63\times5}{9}$
$C=35$
因此，摄氏度温度为$35^o$。
(iv) 温度为$0^o\ C$，
这意味着：
$C=0$
将$C$代入线性方程$F=(\frac{9}{5})C+32$
我们得到：
$F=(\frac{9}{5})0+32$
$F=0+32$
$F=32$
因此，华氏度温度为$32^o$。
温度为$0^oF$
这意味着：
$F = 0$
将$F$代入线性方程$F=(\frac{9}{5})C+32$
我们得到：
$0=(\frac{9}{5})C+32$
$(\frac{9}{5})C=-32$
$C=\frac{-32\times5}{9}$
$C=-17.777$
$C≈-17.8$
因此，摄氏度温度为$-17.8^o$。
(v) 华氏度和摄氏度数值相同的温度
这意味着：
$F=C$
$C=(\frac{9}{5})C+32$
$C-(\frac{9}{5})C=32$
$\frac{(5-9)C}{5}=32$
$(\frac{-4}{5})C=32$
$C=\frac{-32\times5}{4}$
$C=-40$
因此，
华氏度和摄氏度数值相同的温度为$-40^o$。
浏览量：87
