数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究Java程序：将矩阵向右旋转K次
数组是一种线性数据结构，用于存储具有相似数据类型的元素组。它以顺序方式存储数据。当我们创建二维数组（即行和列）时，我们称之为矩阵。
在本文中，我们将创建一个MxN矩阵，并尝试将其向右旋转K次。这里，“M”和“N”分别是行和列的大小。“K”是我们要旋转矩阵的次数。
矩阵向右旋转
让我们通过以下视觉表示来理解什么是矩阵旋转：
示例1
当我们将矩阵旋转1次：
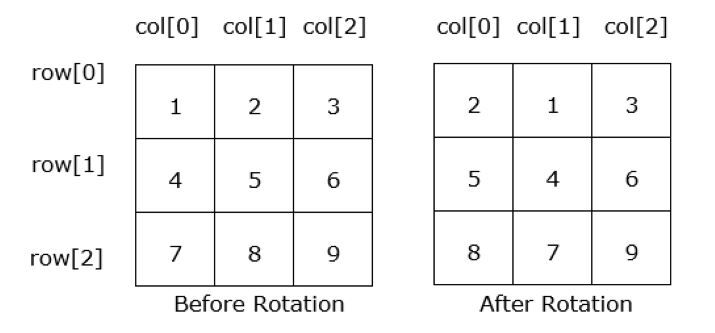
示例2
当我们将矩阵旋转2次：
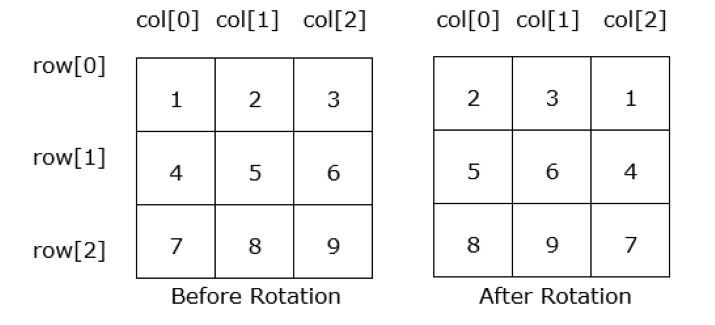
从上图中我们可以看到，当我们将矩阵向右旋转1次时，第一列移到第2个位置；当我们将矩阵向右旋转2次时，第一列移到第3个位置。
矩阵语法
Data_Type matrix_name[ row ][ column ];
// declaration
Or,
// declaration with size
Data_Type matrix_name[ row ][ column ] = new Data_Type[sizeofarray];
Or,
// declaration and initialization
Data_Type matrix_name[ row ][ column ] = { {values separated by comma} };
我们可以在程序中使用以上任何语法。
算法
让我们讨论一下我们将如何旋转给定矩阵的方法。
步骤1 - 我们将创建四个整数值“row”和“column”（大小为4）。第三个整数值为“K”（旋转次数），第四个名为“temp”（临时存储值）。
步骤2 - 声明并初始化一个二维数组arr[][]。
步骤3 - 现在，我们将使用一个while循环，该循环将运行“k % col”次，即旋转次数。当我们旋转数组超过“col”次时，旋转不会影响原始数组。
步骤4 - 在while循环内，我们将使用两个for循环，第一个循环将运行到行的size，并且在每次迭代中，它会将矩阵最后一列的值存储到“temp”变量中。第二个for循环将获取剩余的列值并将其向右移动。
步骤5 - 第二个for循环执行完毕后，我们将“temp”变量的值存储到矩阵的第一列。
步骤6 - 当两个for循环都完成执行后，我们将k减1。之后，我们将检查k是否大于0。如果大于0，则for循环将再次重复执行，并按步骤4和5中所述工作。
在下一节中，我们将看到上述方法的实现。
将矩阵向右旋转K次的程序
示例
public class Mat {
public static void main(String[] args) {
int row=4;
int col=4;
int arr[][] = {{7, 2, 1, 3}, {6, 1, 3, 7}, {4, 9, 8, 0}, {8, 0, 1, 2}};
int k = 3 % col; // Number of rotation
int temp;
System.out.println("The given matrix: ");
// loop to print matrix value
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
// loop to perform matrix rotation
while(k > 0){
for( int i = 0; i < row; i++) {
temp = arr[i][col-1];
// storing last column value to temp
for(int j = col-1; j > 0; j--) {
// reverse loop
arr[i][j] = arr[i][j-1];
// shifting column value to right
}
arr[i][0] = temp;
// storing temp value to array again
}
k--; // decementing k
}
System.out.println("After rotating the given matrix " );
// loop to print new matrix value
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
}
输出
The given matrix: 7 2 1 3 6 1 3 7 4 9 8 0 8 0 1 2 After rotating the given matrix 2 1 3 7 1 3 7 6 9 8 0 4 0 1 2 8
结论
在本文中，我们了解了什么是矩阵以及如何声明和初始化它以便我们可以使用矩阵。此外，我们还讨论了一个Java程序，用于将矩阵旋转k次。
471 次浏览
