NumPy 中的 Kaiser 窗 - Python

---

NumPy 中的 Kaiser 窗 – Python：简介

Kaiser 窗是信号处理和数据分析中一种典型的窗函数。它在频谱分析、滤波器设计和加窗傅里叶变换等应用中发挥着重要作用。Kaiser 窗是一种流行的窗函数，在许多信号处理和数据分析应用中至关重要。在任何应用中，包括频谱分析、滤波器设计和加窗傅里叶变换，Kaiser 窗都提供了一种通用且适应性强的工具来管理主瓣宽度和旁瓣电平之间的权衡。

Kaiser 窗显著减少了频谱泄漏伪影和信号泄漏，从而提高了数据分析方法的精度和可靠性。为了展示 Kaiser 窗在 Python 编程中的强大功能和适应性，本文将探讨其概念、语法、在 NumPy 中的实现以及实际应用。

NumPy 中的 Kaiser 窗 - Python

Kaiser 窗的定义

Kaiser 窗，也称为 Kaiser-Bessel 窗，是一种参数化的窗函数，可以管理主瓣宽度和旁瓣电平之间的权衡。它的目的是减少泄漏，泄漏发生在频谱分析期间感兴趣的信号分散到相邻频率区间时。

语法

可以使用 NumPy 中的 numpy.kaiser 函数创建 Kaiser 窗，其语法如下：

numpy.kaiser(M, beta, sym=True)

其中，M 表示窗口长度，beta 决定其形状，sym 指定窗口是否应是对称的。

语法解释

• 'M' − 窗口长度，通常为大于零的正整数。

• ‘beta’ − Kaiser 窗的形状参数。它控制着旁瓣电平和主瓣宽度之间的权衡。较小的 beta 值会使主瓣变宽并增加旁瓣，而较大的 beta 值会导致主瓣变窄但旁瓣更高。通常，它是一个正实数。

• ‘sym’ − 一个可选参数，控制窗口是否应是对称的。如果设置为 True，则生成的窗口将是对称的。

算法

• 步骤 1 − 导入必要的库

• 步骤 2 − 定义 Kaiser 窗的参数

• 步骤 3 − 使用 ‘numpy.kaiser’ 生成 Kaiser 窗

• 步骤 4 − 绘制 Kaiser 窗

• 步骤 5 − 检查生成的窗口图，以了解旁瓣电平和主瓣宽度如何相互影响。

方法

• 方法 1 − 用于频谱分析的 Kaiser 窗

• 方法 2 − 用于滤波器设计的 Kaiser 窗

方法 1：用于频谱分析的 Kaiser 窗

示例

import numpy as np
import matplotlib.pyplot as plt

# Generate a signal
N = 1024  # Number of samples
fs = 1000  # Sampling frequency
t = np.arange(N) / fs
f = 10  # Frequency of the signal
signal = np.sin(2 * np.pi * f * t)

# Apply the Kaiser window
window = np.kaiser(N, beta=10)
windowed_signal = signal * window

# Perform Fourier transform
spectrum = np.fft.fft(windowed_signal)
freq = np.fft.fftfreq(N, 1 / fs)

# Plot the spectrum
plt.plot(freq, np.abs(spectrum))
plt.title('Kaiser Window Spectrum Analysis')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.grid(True)
plt.show()

输出

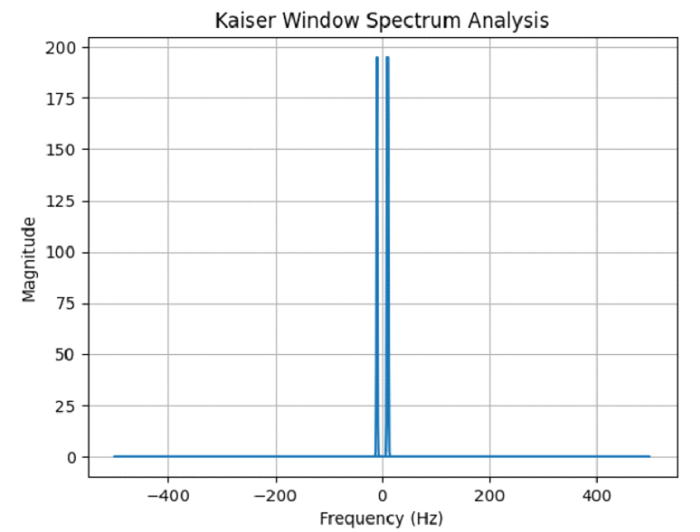
方法 1 的解释

在这种方法中，我们使用 Kaiser 窗分析给定信号的频谱。我们将 Kaiser 窗应用于生成的正弦信号。然后对加窗信号应用傅里叶变换以获得频谱。通过查看生成的频谱图，我们可以检查信号的频谱特性，包括主瓣宽度和旁瓣电平。

应用 Kaiser 窗后，正弦信号的频谱图将是提供的代码的输出。图表的纵轴显示频谱的幅度，而横轴表示以 Hz 为单位的频率。

生成的图形将显示主瓣宽度和旁瓣电平以及信号的其他频谱特性。Kaiser 窗的特性，如窗口长度和形状参数 (beta)，将决定主瓣和旁瓣的确切形状和分布。

在处理信号时，例如检测主要频率或滤除不需要的频率，您可以通过分析图表来识别信号中存在的频率成分及其幅度。

方法 2：用于滤波器设计的 Kaiser 窗

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Filter specifications
N = 101  # Filter order
fs = 1000  # Sampling frequency
fc = 100  # Cutoff frequency
taps = signal.firwin(N, fc, fs=fs, window=('kaiser', 8))

# Plot the filter coefficients
plt.stem(taps)
plt.title('Kaiser Window FIR Filter Coefficients')
plt.xlabel('Tap')
plt.ylabel('Magnitude')
plt.grid(True)
plt.show()

输出

在此方法中，Kaiser 窗用于设计有限脉冲响应 (FIR) 滤波器。我们指定所需的截止频率、采样频率和滤波器阶数。将 Kaiser 窗应用于 scipy.signal.firwin 函数以生成滤波器系数。然后通过绘制生成的滤波器系数来显示频率响应特性。

使用 Kaiser 窗生成的 FIR 滤波器的滤波器系数的茎状图将是给定代码的输出。图表的横轴显示抽头索引，而纵轴显示滤波器系数的大小。

茎状图显示了滤波器系数的幅度值，也显示了滤波器的频率响应特性。选择的滤波器阶数、截止频率和应用于 Kaiser 窗的形状参数 (beta) 将决定系数的确切形状和值。

您可以通过检查图表来了解通带特性、阻带衰减和总体滤波器形状，该图表显示了设计的滤波器的频率响应。此信息可用于信号滤波、降噪和信号重建等应用。

结论

Kaiser 窗是一种灵活的信号处理和数据分析工具，可以控制主瓣宽度和旁瓣电平。本文介绍了 NumPy 中 Kaiser 窗的定义和语法。此外，我们还使用两个实际方法演示了它在频谱分析和滤波器设计中的应用。通过理解和有效地利用 Kaiser 窗，您可以改进您的 Python 信号处理和分析任务。