数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究Python 中 Meshgrid 和 Numpy 的用途
Python 科学计算环境是一个蓬勃发展且活跃的领域，它使科学家、工程师和数据分析师能够有效地执行具有挑战性的计算和分析。它包含各种各样的库和工具，旨在处理诸如数值计算、数据处理和可视化等任务。
Meshgrid 和 Numpy 是这个生态系统中重要的组成部分，它们在操作数组方面至关重要。用户可以使用 Meshgrid 创建坐标网格，这提供了一种处理多维数据分析的实用方法。另一方面，功能强大的库 Numpy 提供了有效的方法来操作、存储和计算大型数组。通过 meshgrid 和 Numpy 的组合优势，用户可以在数组上执行复杂的运算并以全面的方式可视化数据。
了解 Numpy
Numpy（代表 Numerical Python）是一个强大的库，它是 Python 科学计算能力的基础。它包含各种各样的函数，旨在执行数值计算和大型数据处理。使用 Numpy，您可以有效地处理和存储数组，执行矢量化运算以提高速度，并利用大量数学函数进行复杂的计算。
Numpy 具有用户友好的界面并易于与其他科学库集成，因此对于希望快速有效地解决数值问题的研究人员、数据科学家和工程师来说，它是一个宝贵的资源。
特征
Numpy 数组必须是同构的，以便存储相同数据类型的数据项。这种同构性使得内存利用率高效，并且可以优化计算。
Numpy 数组支持任意数量的维度，因此可以表示复杂的数据结构。从一维向量到多维矩阵，Numpy 都能轻松处理它们。
Numpy 的广播功能简化了跨不同形状数组的操作。它会自动复制或扩展数组以匹配形状，从而允许逐元素操作而无需明确定义循环。
为了快速访问和修改数组的元素或部分，Numpy 提供了简单的索引和切片功能。这使得能够以多种方式提取和修改数据。
了解 Meshgrid
Meshgrid 是科学计算中的一个基本概念，对于构建坐标网格至关重要。通过将一个或多个 1D 数组转换为两个等效的 2D 数组，Meshgrid 允许进行多维数据分析。这个强大的工具使各种数学和图形运算成为可能，使学术界和数据科学家能够从大量数据中提取有价值的见解。
使用 meshgrid 可以大大简化构建坐标网格的过程。它会根据提供的坐标向量自动生成坐标矩阵。生成的矩阵显示了每个网格点的 X 和 Y 坐标。这种无缝的网格创建允许进行简单的处理和数据分析。Meshgrid 是一个基础构建块，可以用于执行各种任务，例如创建等值线图、可视化数学函数和显示矢量场。
Numpy 和 meshgrid 在 Python 中的作用
meshgrid 和 Numpy 的组合极大地增强了 Python 执行复杂数据分析和数组操作的能力。Meshgrid 简化了创建坐标网格的过程，以便更轻松地分析多维数据。它会自动生成 X 和 Y 坐标矩阵，从而简化了网格上的数据操作和分析。
另一方面，Numpy 为有效地操作、存储和计算数组提供了基础。Numpy 强大的数组操作和数学函数使研究人员和数据科学家能够在数组上执行复杂的运算并从数据中获得有意义的见解。
示例
这是一个完整的 Python 函数代码示例，演示了如何使用 Numpy 和 meshgrid()。
import numpy as np
import matplotlib.pyplot as plt
# Generating a meshgrid using meshgrid() function
x = np.linspace(-5, 5, 100) # 1D array for x coordinates
y = np.linspace(-5, 5, 100) # 1D array for y coordinates
X, Y = np.meshgrid(x, y) # Generating the meshgrid
# Defining a mathematical function to visualize
Z = np.sin(np.sqrt(X**2 + Y**2)) / (np.sqrt(X**2 + Y**2))
# Plotting the function using matplotlib
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.title('3D Surface Plot of a Mathematical Function')
plt.show()
输出
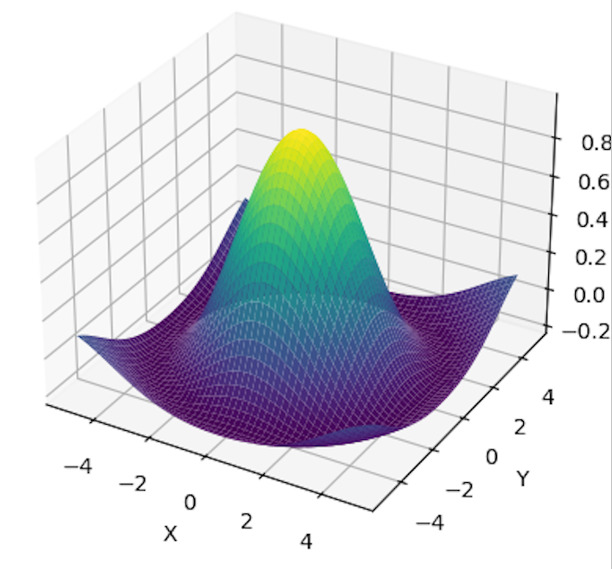
在这个示例中，我们首先加载两个先决条件库：Numpy 和 Matplotlib。接下来，使用 numpy 的 linspace() 函数定义 x 和 y 坐标的范围。我们使用 numpy 的 meshgrid() 方法将 x 和 y 坐标组合起来创建网格，并将生成的网格存储在 X 和 Y 变量中。然后，我们创建一个数学函数 Z，我们希望在这个网格上显示它。然后，使用我们之前生成的 meshgrid，我们使用 matplotlib 创建数学函数的 3D 表面图。
结论
在这篇文章中，我们探讨了 Numpy 和 meshgrid() 在 Python 科学计算环境中的功能和用法。Numpy 提供了经济的存储、快速的计算和广泛的数学函数集，从而可以进行数组操作。meshgrid() 简化了网格的创建，用于诸如可视化、插值和积分等任务。通过将 Numpy 的能力与 meshgrid() 的网格生成能力相结合，我们可以进行复杂的数据分析并解决具有挑战性的问题。
浏览量 138 次
