电磁铁的磁场强度

磁场强度是指作用在一个位于磁场中一点的单位测试北极（即 1 Wb 的 N 极）上的力。用 H 表示。

磁场强度是一个矢量，具有大小和方向。

磁场强度也称为磁化力、磁场强度和磁势梯度等。

解释

考虑一个位于距离 m Wb 磁极 r 米处的 x 点。假设在 x 点放置一个单位北极（即 1 Wb 的磁极）。

因此，根据定义，x 点的磁场强度是在 x 点放置的单位北极所受的力，即：

x 点的磁场强度，H = 作用在 x 点单位北极上的力

因此，根据库仑磁力定律：

$$\mathrm{H=\frac{1}{4\pi\:\mu_{0}\mu_{r}}(\frac{m_{1}m_{2}}{r^{2}})=\frac{1}{4\pi\:\mu_{0}}(\frac{m\times\:1}{r^{2}})\:\:\:\:\:(\because\:\mu_{r(air)}=1)}$$

$$\mathrm{\Rightarrow\:H=\frac{1}{4\pi\:\mu_{0}}(\frac{m}{r^{2}})\:\:\:...(1)}$$

因此，公式 (1) 给出了位于强度为 m Wb 磁极磁场中的 x 点的磁场强度。

磁场强度的单位

根据磁场强度的定义，我们可以写成：

$$\mathrm{H=作用在磁极上的力=\frac{力(F)}{磁极强度 (𝑚)=\frac{牛顿}{韦伯}}=N/Wb}$$

因此，磁场强度以牛顿每韦伯 (N/Wb) 为单位。

电磁铁的磁场强度

电磁铁是在磁性材料芯上绕制的线圈。

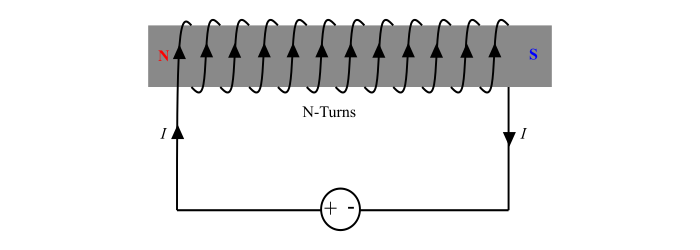
考虑一个 N 匝线圈，流过它的电流为 I 安培，则

磁场强度为：

$$\mathrm{H=\frac{NI}{l}\:\:AT/m\:\:\:...(2)}$$

其中：

• NI 称为磁动势 (mmf)，

• l 是磁路的长度（米）。

公式 (2) 定义了AT/m作为磁场强度的单位，它等效于N/Wb。

重要提示 - 磁场强度也可以用磁通密度 (B) 表示如下：

$$\mathrm{B=\mu_{0}\mu_{r}H}$$

$$\mathrm{\Rightarrow\:H=\frac{B}{\mu_{0}\mu_{r}}\:\:\:...(3)}$$

数值示例 (1)

一个磁极的强度为 100 mWb，放置在真空中产生磁场。确定磁场中距离磁极 2 米的 x 点的磁场强度。

解 −

由于磁极放置在真空中，因此磁场强度为：

$$\mathrm{H=\frac{1}{4\pi\:\mu_{0}}(\frac{m}{r^{2}})=\frac{1}{4\pi\:(4\pi\times\:10^{-7})}(\frac{100\times\:10^{-3}}{2^{2}})}$$

$$\mathrm{\Rightarrow\:H=1.584\times\:10^{3}\:N/Wb}$$

数值示例 (2)

一个环形线圈的磁路长度为 40 cm，线圈匝数为 600 匝。线圈电流为 200 mA。计算线圈产生的磁场强度。

解 −

对于线圈，磁场强度由下式给出：

$$\mathrm{H=\frac{NI}{l}=\frac{600\times\:200\times\:10^{-3}}{40\times\:10^{-2}}=300\:AT/m}$$

数值示例 (3)

当气隙中的磁通密度等于 0.05 T 时，确定磁场强度。

解 −

这里，气隙中的磁场强度为：

$$\mathrm{H=\frac{B}{\mu_{0}}=\frac{0.05}{4\pi\:\times10^{-7}}=3.981\times\:10^{4}\:AT/m}$$

Saini Manish Kumar

更新于：2021年7月5日

2K+ 次浏览

开启你的职业生涯

完成课程获得认证

开始学习