偶极子均匀磁场

---

引言

当磁铁置于磁场中时，会受到力的作用。磁场是一个用来描述对磁性材料影响的物理场。磁场的均匀性对其附近的偶极子有特殊的影响。学习作用在偶极子上的力和力矩的性质，并进一步理解其背后的原因非常重要。另一个有趣的方面是，磁偶极子在磁场中的类似关系与电偶极子在电场中的关系也将会推导和探讨。

什么是均匀磁场？

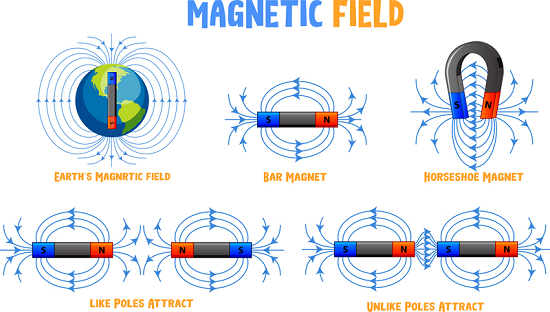
这是一个矢量场，它解释了磁性影响和力对任何类型的磁性材料或其附近的运动电荷的影响。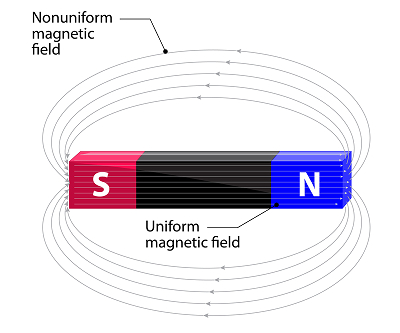磁场可以通过磁铁、运动电荷或电流产生。由于它是矢量，所以需要大小和方向来完整描述它。我们经常使用“场线”图来了解空间中产生的场。条形磁铁的磁场线表示如图所示。较近的场线表示该区域较高的强度。箭头表示磁场的方向。

均匀磁场仅仅意味着场的大小和方向在我们考虑的整个区域内都是相同的。大小或方向不会随着空间坐标的变化而变化。均匀磁场在任何特定区域的场线密度将告诉我们磁场的大小。

什么是偶极子？

一般来说，偶极子是两个大小相等、极性相反的带电或磁化极点以一定距离排列。带电荷的排列称为电偶极子，而带有南北极的排列称为磁偶极子。

偶极矩是一个物理矢量量，可以用它轻松地表征任何类型的偶极子——无论是磁偶极子还是电偶极子。对于电偶极子，偶极矩只是电荷大小与其之间距离的乘积。而磁偶极子是产生磁场的任何物体的强度和方向的表示。简单的条形磁铁是具有永久磁矩的磁偶极子的例子。甚至原子中带正电的原子核的自旋、带负电的电子绕原子核的旋转等等，也是构成磁偶极矩的例子。

偶极子在均匀磁场中的行为

当我们将北极带入磁场时（尽管我们不能带入孤立的磁极），它会受到一个力，该力等于磁强度和磁场值的乘积。数学上可以表示为：

$$\mathrm{F= m\times B}$$

这里m是磁极强度，B是磁场的大小。而南极则受到大小相等、方向相反的力。因此，偶极子没有受到净力。但是，需要注意的重要一点是，这两个力作用在相距一定距离（例如“2l”）的地方。（“2l”表示两个磁极之间的距离，我们可以说这是放在均匀磁场B中的小条形磁铁的长度）这导致偶极子产生净力矩。数学上，它由下式给出：

$$\mathrm{\tau = 力\times 距离}$$

$$\mathrm{\tau_{B} = mB\:sin\theta \times 2l}$$

将2ml作为磁矩矢量“M”，我们得到力矩公式为

$$\mathrm{\tau_{B} = M\times B}$$

此外，在计算系统的势能时，

$$\mathrm{U_{B} = \int \tau _{B}(\theta )d\theta }$$

$$\mathrm{U_{B} = \int MB\:sin \theta \:d\theta }$$

$$\mathrm{U_{B} = - MB\:cos \theta }$$

$$\mathrm{U_{B} = - M.B}$$

与静电学的关联

可以将磁静力学中偶极子在均匀磁场中的力和力矩以及其他行为效应与静电学中的进行比较。正如我们已经推导出均匀磁场中磁偶极子的力矩公式一样，均匀电场中电偶极子的力矩公式也是如此。矩m类似于p。磁极强度m类似于电荷q。此外，我们用电场E代替磁场B。

数学上，它由下式给出

$$\mathrm{\tau _{E}=力\times 距离}$$

$$\mathrm{\tau _{E}=q\:E\:sin\theta \times 2l}$$

将2ql作为磁矩矢量“p”，我们得到力矩公式为

$$\mathrm{\tau _{E}=p\times E}$$

此外，在计算系统的势能时，

$$\mathrm{U _{E}=\int T_{E}(\theta )d\theta }$$

$$\mathrm{U _{E}=\int pE\:sin\theta \:d\theta }$$

$$\mathrm{U _{E}=-ME\:cos\theta}$$

$$\mathrm{U _{E}=-M.E}$$

因此，我们看到当分别置于均匀电场和磁场中时，电偶极子和磁偶极子之间存在明显的相似性。负号为我们提供了这样一个约定：对抗电场（或磁场）所做的功增加了系统的势能。

结论

电偶极子和磁偶极子都简单来说是大小相等、极性相反的极点以一定距离排列。当放在均匀磁场中时，尽管没有受到任何净力，但它们会经历一些力矩。对于均匀磁场中磁偶极子的力矩和势能的表达式，与均匀电场中电偶极子的表达式非常类似。这为我们打开了学习磁静力学和静电学之间这种类似关系的许多其他有趣方面的大门。

常见问题

Q1. 均匀磁场线的性质是什么？

A1. 均匀磁场线是等距平行线。

Q2. 洛伦兹力是什么意思？

A2. 当电荷q以速度v进入具有电场E和磁场B的区域时，其上的净力F。数学上由下式给出

$$\mathrm{F=q[E+(v\times B)]}$$

Q3. 磁矩是标量还是矢量？

A3. 磁矩是矢量。其方向指向磁性材料的南极到北极。

对于载流环路，根据右手定则，其方向平行于平面——手指沿电流方向弯曲。

Q4. H和B有什么区别？

A4. H是磁场强度，单位为A/m。而磁通密度B的单位为特斯拉。

Q5. 从均匀场区域无偏转通过的电子上的电力与磁力的比例是多少？

A5. 由于电子在该区域内未发生偏转，因此作用在其上的电力和磁力的值相等且方向相反。因此，这两个力的比率为1。