由两相电源产生的旋转磁场

单相电源产生脉动的磁场，该磁场不会在空间旋转。因此，单相电源无法在静止转子上产生旋转。然而，与三相电源一样，两相电源也可以产生恒定幅值的旋转磁场。因此，除阴影极感应电动机外，所有单相感应电动机都作为两相电动机启动。一旦启动，电动机将继续在单相电源下运行。

两相电源如何产生恒定幅值的旋转磁场？

考虑一个两相、两极电动机，其中A相和B相由平衡的两相电源供电，这些相中的电流分别为I_A和I_B，如图所示。

很明显，电流I_A比电流I_B超前90°。因此，这些电流产生的磁通量可以写成：

$$\mathrm{φ_{𝐴} = φ_{𝑚}\:sin(\omega 𝑡 + 90°) = φ_{𝑚}\:cos\:\omega 𝑡 … (1)}$$

$$\mathrm{φ_{𝐵} = φ_{𝑚}\:sin\:\omega 𝑡 … (2)}$$

其中，φ_m是任一相电流产生的磁通量的最大值。

我们现在将证明，这个两相电源产生一个在空间旋转的恒定幅值的磁通量。

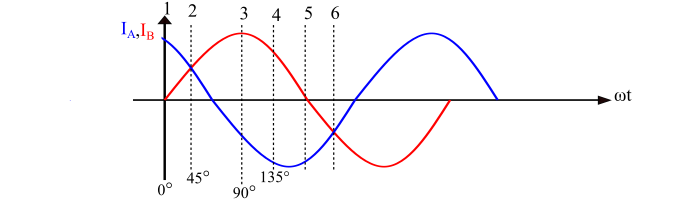
时刻1

参考电流I_A和I_B的波形。在这里，在时刻1，B相中的电流为零，而A相中的电流为正最大值。时刻1对应于ωt = 0°，因此，磁通量由下式给出：

$$\mathrm{φ_{𝐴} = φ_{m}\:cos\:\omega 𝑡 = φ_{m}\:cos\:0 = φ_{m}}$$

以及

$$\mathrm{φ_{𝐵} = φ_{m}\:sin\:\omega 𝑡 = φ_{m}\:sin\:0 = 0}$$

因此，时刻1的合成磁通量为

$$\mathrm{φ_{𝑅} = \sqrt{{φ^{2}_{𝐴}}+{φ^{2}_{B}}}=\sqrt{(φ_{𝑚})^{2}+(0)^{2}}= φ_{𝑚}}$$

因此，合成磁通量的幅值等于φ_m，并指向右侧，如图时刻1所示。

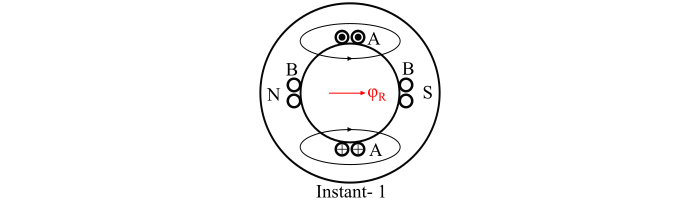
时刻2

在这个时刻，A相中的电流仍然沿相同方向流动，并且B相中也流有等量的电流。这个时刻对应于ωt = 45°，因此：

$$\mathrm{φ_{𝐴} = φ_{m}\:cos\:\omega 𝑡 = φ_{m}\:cos\:45 =\frac{1}{\sqrt{2}}φ_{m}}$$

以及

$$\mathrm{𝜑_{𝐵} = 𝜑_{𝑚}\:sin\:\omega 𝑡 = 𝜑_{𝑚} \:sin\:45 =\frac{1}{\sqrt{2}}φ_{m}}$$

因此，合成磁通量由下式给出：

$$\mathrm{𝜑_{𝑅} =\sqrt{{φ^{2}_{𝐴}}+{φ^{2}_{B}}}=\sqrt{(\frac{φ_{m}}{\sqrt{2}})^{2}+(\frac{φ_{m}}{\sqrt{2}})^{2}}=φ_{m}}$$

因此，合成磁通量具有相同的数值，但相对于时刻1顺时针旋转了45°（参见时刻2的图）。

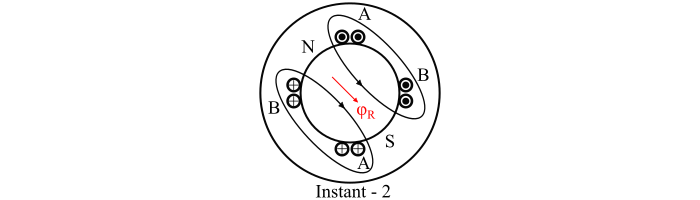
时刻3

在时刻3，A相中的电流减小到0，而B相中的电流增加到正最大值。这个时刻对应于波形图中的ωt = 90°，因此：

$$\mathrm{φ_{𝐴} = φ_{m}\:cos\:ωt = φ_{m}\:cos\:90 = 0}$$

以及

$$\mathrm{𝜑_{𝐵} = φ_{m}\:sin\:ωt = φ_{m}\:sin\:90 = φ_{m}}$$

因此，合成磁通量由下式给出：

$$\mathrm{𝜑_{𝑅} =\sqrt{{φ^{2}_{𝐴}}+{φ^{2}_{B}}}=\sqrt{({0})^{2}+({φ_{m}})^{2}}=φ_{m}}$$

因此，合成磁通量再次具有相同的幅值，等于**φ_m**，但是相对于时刻1顺时针旋转了90°（参见时刻3的图）。

时刻4

在时刻4，A相中的电流反向，其值与B相中的电流相同（电流I_B为正）。这个时刻对应于ωt = 135°，因此磁通量由下式给出：

$$\mathrm{𝜑_{𝐴} = 𝜑_{𝑚}\:cos\:ωt = 𝜑_{𝑚} \:cos\:135 =-\frac{1}{\sqrt{2}}𝜑_{𝑚}}$$

以及

$$\mathrm{𝜑_{𝐵} = 𝜑_{𝑚}\:cos\:ωt = 𝜑_{𝑚} \:cos\:135 =\frac{1}{\sqrt{2}}𝜑_{𝑚}}$$

因此，合成磁通量由下式给出：

$$\mathrm{𝜑_{𝑅} =\sqrt{{φ^{2}_{𝐴}}+{φ^{2}_{B}}}=\sqrt{(-\frac{φ_{m}}{\sqrt{2}})^{2}+(\frac{φ_{m}}{\sqrt{2}})^{2}}=φ_{m}}$$

同样，合成磁通量具有相同的幅值，但是相对于时刻1旋转了135°，如图时刻4所示。我们将继续考虑其他时刻来证明这一事实。

从以上讨论可以看出，平衡的两相电源产生一个等于**φ_m**的恒定值的旋转磁场。磁场旋转的速度称为**同步速度**，由下式给出：

$$\mathrm{𝑁_{𝑆} =\frac{120𝑓}{𝑃}}$$

其中：

• P是机器中的极数，以及
• f是电源频率。

Saini Manish Kumar

更新于：2021年9月24日

2K+ 次浏览

启动您的职业生涯

完成课程获得认证

开始