数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究三相感应电动机中的旋转磁场
当三相电源馈送到三相感应电动机的定子绕组时，会产生旋转磁场 (RMF)。该磁场使得其磁极不会停留在定子上固定的位置，而是不断地围绕定子改变其位置。因此，它被称为旋转磁场 (RMF) 或 RMF。
在数学上，可以证明该旋转磁场的幅值是恒定的，并且等于任何相位电流产生的最大磁通量 (ϕm) 的 1.5 倍。
旋转磁场的速度称为同步速度 (NS)。同步速度的值取决于定子上的磁极数 (P) 和电源频率 (f)。因此，
$$\mathrm{同步速度, 𝑁_𝑆 =\frac{120 𝑓}{𝑃}RPM}$$
旋转磁场的数学分析
考虑三个相同的线圈，它们在空间上彼此相隔 120°。假设这三个线圈由平衡的三相电源供电。因此，每个线圈都会在其自身轴线上产生交变磁通量。现在，假设三个瞬时磁通量分别为：
$$\mathrm{\varphi_1 = \varphi_m sin \omega t … (1)}$$
$$\mathrm{\varphi_2 = \varphi_m sin(\omega t − 120°) … (2)}$$
$$\mathrm{\varphi_3 = \varphi_m sin(\omega t + 120°) … (3)}$$
这里，ϕm 是任何相位电流产生的磁通量的最大值。相量图显示了这三个磁通量。
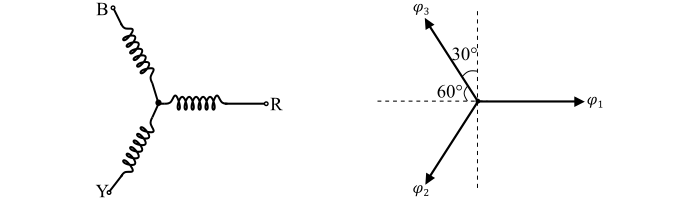
为了确定合成磁通量的幅值，将每个磁通量分解成水平和垂直分量，然后求其相量和。
因此，磁通量的合成水平分量由下式给出：
$$\mathrm{\varphi_h = \varphi_1 − \varphi_2 cos 60° − \varphi_3 cos 60° = \varphi_1 − (\varphi_2 + \varphi_3) cos 60°}$$
$$\mathrm{⇒ \varphi_h = \varphi_1 −\frac{1}{2}(\varphi_2 + \varphi_3)}$$
$$\mathrm{⇒ \varphi_h = (\varphi_m sin \omega t) −\frac{1}{2}[\varphi_m sin(\omega t − 120°) + \varphi_m sin(\omega t + 120°)]}$$
$$\mathrm{⇒ \varphi_h = (\varphi_m sin \omega t) −\frac{\varphi_m}{2}(sin \omega t\:cos 120° − cos \omega t\:sin 120°+ sin \omega t\:𝑐𝑜𝑠120° + cos \omega t\:sin 120°)}$$
$$\mathrm{⇒ \varphi_h = \varphi_m sin \omega t − [\frac{\varphi_m}{2}× (2 sin \omega t) × (\frac{-1}{2})]}$$
$$\mathrm{⇒ \varphi_h =\frac{3}{2}\varphi_m sin \omega t … (4)}$$
磁通量的合成垂直分量由下式给出：
$$\mathrm{\varphi_v = 0 − \varphi_2 cos 30° + \varphi_3 cos 30° = (−\varphi_2 + \varphi_3) cos 30°}$$
$$\mathrm{⇒ \varphi_v = [−\varphi_m sin(\omega t − 120°) + \varphi_m sin(\omega t + 120°)] cos 30°}$$
$$\mathrm{⇒ \varphi_v =\frac{\sqrt{3}}{2}\varphi_m [−(sin \omega t\:cos 120° − cos \omega t\:sin 120°)+(sin \omega t \:𝑐𝑜𝑠120° + cos \omega t\:sin 120°)]}$$
$$\mathrm{⇒ \varphi_v =\frac{\sqrt{3}}{2}\varphi_m(2 cos \omega t\:sin 120°) =\frac{\sqrt{3}}{2}\varphi_m × (2 cos \omega t) ×\frac{\sqrt{3}}{2}}$$
$$\mathrm{⇒ \varphi_v =\frac{3}{2}\varphi_m cos \omega t … (5)}$$
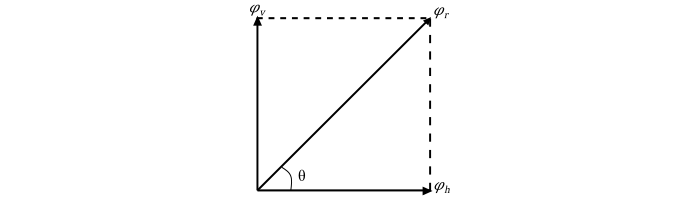
因此，合成磁通量由下式给出：
$$\mathrm{\varphi_r = \sqrt{\varphi_h^2 + \varphi_v^2} = \sqrt{(\frac{3}{2}\varphi_m sin \omega t)^2+ (\frac{3}{2}\varphi_m cos \omega t)^2}}$$
$$\mathrm{⇒ \varphi_r =\frac{3}{2}\varphi_m (\sqrt{sin2 \omega t + cos2 \omega t}) =\frac{3}{2}\varphi_m … (6)}$$
因此，从公式 (6) 可以清楚地看出，合成旋转磁场的幅值等于每相磁通量 (ϕm) 最大值的 1.5 倍。此外，合成磁通量 (ϕr) 与时间无关，即它是恒定磁通量。
再次，
$$\mathrm{tan \theta =\frac{\varphi_v}{\varphi_h}=\frac{(\frac{3}{2}\varphi_m cos \omega t)}{(\frac{3}{2}\varphi_m sin \omega t)}= cot \omega t = tan(90° − \omega t)}$$
$$\mathrm{\therefore \theta = (90° − \omega t) … (7)}$$
公式 (7) 表明该角度是时间的函数。因此，
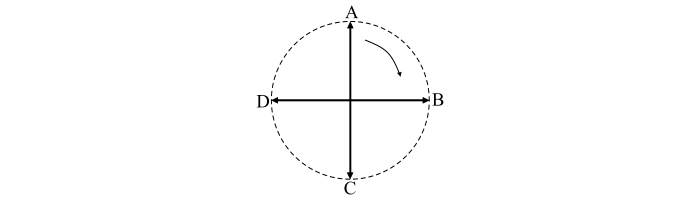
- 情况 1 – 当 ωt = 0° 时；θ = 90°。它对应于上图中的位置 A。
- 情况 2 – 当 ωt = 90° 时；θ = 0°。它对应于位置 B。
- 情况 3 – 当 ωt = 180° 时；θ = -90°。它对应于位置 C。
- 情况 4 – 当 ωt = 270° 时；θ = -180°。它对应于位置 D。
因此，可以看出合成磁通量在空间中以 ω 弧度/秒的角速度沿顺时针方向旋转。因此，对于具有 P 个磁极的机器，
$$\mathrm{\omega = 2𝜋𝑓;\: and\: 𝑓 =\frac{𝑃𝑁_𝑆}{120};}$$
从以上讨论中可以得出以下结论 -
- 平衡三相电源系统的三相电流在电机中产生幅值恒定的合成磁通量。磁通量在每个时刻的幅值为 1.5 ϕm。
- 合成磁通量本质上是旋转的，并且其旋转角速度与电源电流的角速度相同。
- 合成磁通量的旋转方向取决于电源系统的相序。
30K+ 次查看
