三相异步电动机的运行转矩

运行状态下三相异步电动机的转矩

设三相异步电动机静止时转子电路每相电阻为R₂，每相电抗为X₂，每相感应电动势为E₂。如果‘s’是电机运行时的滑差，则：

$$\mathrm{每相转子电抗 , 𝑋′_2 = 𝑠 𝑋_2}$$

$$\mathrm{每相转子电动势 , 𝐸′_2 = 𝑠 𝐸_2}$$

$$\mathrm{\therefore \:每相转子阻抗 , 𝑍′_2 = \sqrt{𝑅_2^2 + (𝑠 𝑋_2)^2}}$$

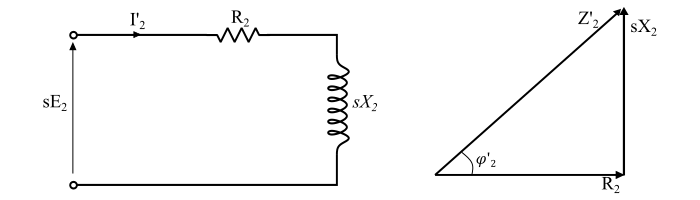
$$\mathrm{每相转子电流 ,𝐼′_2 =\frac{𝐸'_2}{𝑍′_2}=\frac{𝑠𝐸_2}{\sqrt{𝑅_{2}^{2} + (𝑠 𝑋_2)^2}}… (1)}$$

$$\mathrm{转子功率因数, cos \varphi′_2 =\frac{𝑅_2}{𝑍′_2}=\frac{𝑅_2}{\sqrt{𝑅_{2}^{2} + (𝑠 𝑋_2)^2}}… (2)}$$

因此，

$$\mathrm{运行转矩, \tau_𝑟 \propto 𝐸′_2 𝐼′_2 cos \varphi′_2 … (3)}$$

$$\mathrm{\because 𝐸′_2 \propto 磁通 (\varphi)}$$

$$\mathrm{\therefore \tau_𝑟 = 𝐾 \varphi 𝐼′_2 cos \varphi′_2}$$

$$\mathrm{⇒ \tau_𝑟 = 𝐾 \varphi ×\frac{𝑠𝐸_2}{\sqrt{𝑅_{2}^{2} + (𝑠 𝑋_2)^2}}\times\frac{𝑅_2}{\sqrt{𝑅_{2}^{2} + (𝑠 𝑋_2)^2}}}$$

$$\mathrm{⇒ \tau_𝑟 =\frac{𝐾 \varphi 𝑠 𝐸_2 𝑅_2}{𝑅_2^2 + (𝑠 𝑋_2)^2}… (4)}$$

$$\mathrm{\because 𝐸_2 \propto \varphi}$$

$$\mathrm{\therefore \tau_𝑟 =\frac{𝐾 𝑠 𝐸_2^2 𝑅_2}{𝑅_2^2 + (𝑠 𝑋_2)^2}… (5)}$$

公式(4)给出了运行转矩的值。可以看出

• 运行转矩与滑差成正比，即滑差增加，转矩增加，反之亦然。
• 运行转矩与电源电压的平方成正比，因为(E₂ ∝ V)。

由于三相异步电动机的运行转矩由下式给出：

$$\mathrm{\tau_𝑟 =\frac{𝐾 \varphi 𝑠 𝐸_2 𝑅_2}{𝑅_2^2 + (𝑠 𝑋_2)^2}}$$

由于电源电压(V)恒定，则定子磁通以及感应电动势E₂将保持恒定。

$$\mathrm{\therefore \tau_𝑟 =\frac{𝐾_1 𝑠 𝑅_2}{𝑅_2^2 + (𝑠 𝑋_2)^2}… (6)}$$

其中，K1 = K ϕ E₂为常数。

$$\mathrm{⇒ \tau_𝑟 =\frac{𝐾_1 𝑅_2}{\frac{𝑅_2^2}{𝑠}+ 𝑠𝑋_2^2}… (7)}$$

为了使运行转矩最大，公式(6)的分母应最小。因此，对公式(6)的分母关于滑差's'求导，并令其等于零，即：

$$\mathrm{\frac{𝑑}{𝑑𝑠} (\frac{𝑅_2^2}{𝑠}+ 𝑠𝑋_2^2) = 0}$$

$$\mathrm{⇒ −\frac{𝑅_2^2}{𝑠^2}+ 𝑋_2^2 = 0}$$

$$\mathrm{⇒ 𝑅_2 = 𝑠 𝑋_2 … (8)}$$

因此，在运行条件下获得最大转矩时，

$$\mathrm{每相转子电阻= 每单位滑差 × 静止转子每相电抗}$$

现在，

$$\mathrm{\tau_𝑟 \propto\frac{𝑠 𝑅_2}{𝑅_2^2 + (𝑠 𝑋_2)^2}}$$

将R₂ = s X₂代入上述表达式，运行条件下的最大转矩由下式给出：

$$\mathrm{⇒ \tau_𝑟 \propto\frac{1}{2 𝑋_2}… (9)}$$

对应于最大转矩的滑差由下式给出：

$$\mathrm{𝑠_𝑚 =\frac{𝑅_2}{𝑋_2}… (10)}$$

数值例子

一台6极，50Hz，三相异步电动机，每相转子电阻为0.03Ω，静止电抗为0.5Ω。确定对应于最大转矩的滑差和产生最大转矩的电机速度。

解答

(1) 对应于最大运行转矩的滑差为：

$$\mathrm{𝑠_𝑚 =\frac{𝑅_2}{𝑋_2}=\frac{0.03}{0.5}= 0.06}$$

(2) 对应于最大转矩的电机速度为：

$$\mathrm{同步速度, 𝑁_𝑠 =\frac{120𝑓}{𝑃}=\frac{120 \times 50}{6}= 1000 RPM}$$

$$\mathrm{\therefore 𝑁_𝑟 = 𝑁_𝑠(1 − 𝑠_𝑚) = 1000 × (1 − 0.06) = 940 RPM}$$

Saini Manish Kumar

更新于: 2021年8月28日

浏览量5000+

开启你的职业生涯

完成课程获得认证

开始学习