单相单绕组感应电动机性能分析

单相单绕组感应电动机的性能分析可以通过图中所示的等效电路进行。电动机中存在正向和反向功率分量以及转矩分量。

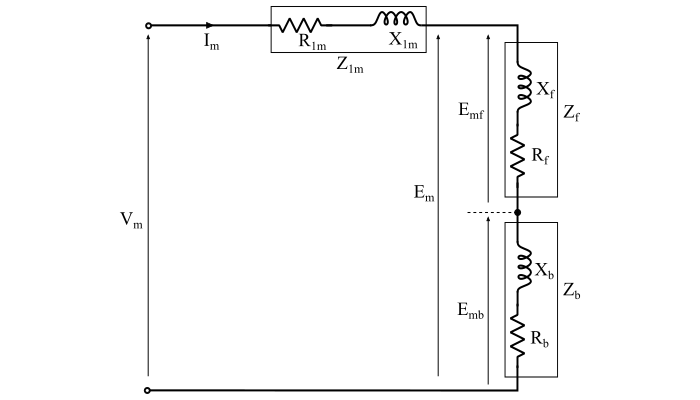
这里，反向磁场的转矩方向与正向磁场方向相反，因此单相感应电动机的总气隙功率由下式给出：

$$\mathrm{𝑃_{𝑔} = 𝑃_{𝑔𝑓} − 𝑃_{𝑔𝑏} … (1)}$$

其中，P_gf 是正向磁场的气隙功率，由下式给出：

$$\mathrm{𝑃_{𝑔𝑓} = {{𝐼}^{2}_{𝑚}}\:𝑅_{𝑓}}$$

而 P_gb 是反向磁场的气隙功率，由下式给出：

$$\mathrm{𝑃_{𝑔𝑏} = {{𝐼}^{2}_{𝑚}}\:𝑅_{b}}$$

因此，总气隙功率也可以表示为：

$$\mathrm{𝑃_{𝑔} = {{𝐼}^{2}_{𝑚}}𝑅_{𝑓} − {{𝐼}^{2}_{𝑚}}𝑅_{b} = {{𝐼}^{2}_{𝑚}}(𝑅_{𝑓} − 𝑅_{𝑏} ) … (2)}$$

现在，正向磁场产生的转矩由下式给出：

$$\mathrm{τ_{𝑓} =\frac{𝑃_{𝑔𝑓}}{𝜔_{𝑠}}=\frac{𝑃_{𝑔𝑓}}{2π 𝑛_{𝑠}}… (3)}$$

反向磁场产生的转矩由下式给出：

$$\mathrm{τ_{b} =\frac{𝑃_{𝑔𝑏}}{𝜔_{𝑠}}=\frac{𝑃_{𝑔b}}{2π 𝑛_{𝑠}}… (4)}$$

其中，

• ω_𝑠 = 同步速度（弧度/秒），以及

• 𝑛_𝑠 = 同步速度（转/秒）。

电动机产生的合成电磁转矩 (τ_e) 等于正向转矩 (τ_f) 和反向转矩 (τ_b) 之差，即：

$$\mathrm{τ_{𝑒} = τ_{𝑓} − τ_{𝑏}}$$

单相感应电动机正向磁场引起的转子铜损由下式给出：

$$\mathrm{𝑃_{𝑟𝑐𝑢.𝑓} = 𝑠𝑃_{𝑔𝑓} … (5)}$$

单相感应电动机反向磁场引起的转子铜损由下式给出：

$$\mathrm{𝑃_{𝑟𝑐𝑢.𝑏} = (2 − 𝑠)𝑃_{𝑔𝑏} … (6)}$$

因此，单相感应电动机的总转子铜损由下式给出：

$$\mathrm{𝑃_{𝑟𝑐𝑢} = 𝑠𝑃_{𝑔𝑓} + (2 − 𝑠)𝑃_{𝑔𝑏} … (7)}$$

单相感应电动机中转换成机械功率的电功率由下式给出：

$$\mathrm{𝑃_{𝑚} = ω τ_{𝑒} … (8)}$$

其中，ω 是以弧度/秒为单位测量的转子角速度。

因为，

$$\mathrm{ω = (1 − 𝑠) × ω_{𝑠}}$$

$$\mathrm{∴\:𝑃_{𝑚} = (1 − 𝑠) × ω_{𝑠}τ_{𝑒}}$$

$$\mathrm{\Rightarrow\:𝑃_{𝑚} = (1 − 𝑠) × 𝑃_{𝑔} = {𝐼^2_{𝑚}} (1 − 𝑠)(𝑅_{𝑓} − 𝑅_{𝑏 }) … (9)}$$

因此，电机轴上可用的功率由下式给出：

$$\mathrm{𝑃_{out} = 𝑃_{𝑚} − 𝑃_{core\:loss} − 𝑃_{𝑓𝑤} − 𝑃_{stray\:losses}}$$

其中，P_fw 是摩擦和风损。

$$\mathrm{∵\:𝑃_{rot.} = 𝑃_{core\:loss} + 𝑃_{𝑓𝑤}}$$

$$\mathrm{∴\:𝑃_{out} = 𝑃_{𝑚} − 𝑃_{rot.} − 𝑃_{stray\:losses} … (10)}$$

Saini Manish Kumar

更新于：2021年9月24日

浏览量：1000+

开启您的职业生涯

完成课程获得认证

开始学习