数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中将木板切割成正方形的最小成本
概念
假设给定一块长为 p、宽为 q 的木板，我们需要将其切割成 p*q 个正方形，使得切割成本最小。对于这块木板，每条边的切割成本将被给出。简而言之，我们需要选择一个切割序列，使得成本最小化。
示例
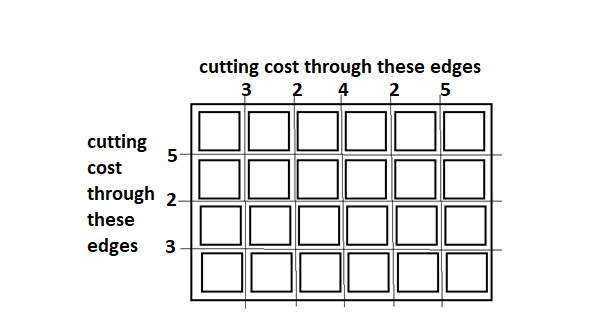
关于上述木板，将其切割成正方形的最佳方式是：
上述情况下的总最小成本为 65。它是通过实现以下步骤计算得出的。
Initial Value : Total_cost = 0 Total_cost = Total_cost + edge_cost * total_pieces Cost 5 Horizontal cut Cost = 0 + 5*1 = 5 Cost 5 Vertical cut Cost = 5 + 5*2 = 15 Cost 4 Vertical cut Cost = 15 + 4*2 = 23 Cost 3 Horizontal cut Cost = 23 + 3*3 = 32 Cost 3 Vertical cut Cost = 32 + 3*3 = 41 Cost 2 Horizontal cut Cost = 41 + 2*4 = 49 Cost 2 Vertical cut Cost = 49 + 2*4 = 57 Cost 2 Vertical cut Cost = 57 + 2*4 = 65
方法
这种类型的问题可以通过实现贪婪算法来解决。如果总成本用 S 表示，则 S = b1x1 + b2x2 … + bkxk，其中 xi 表示某条边切割的成本，bi 是相应的系数，系数 bi 由我们在切割过程结束时通过边 xi 完成的切割总数决定。
我们应该注意到系数的总和始终是常数，因此我们希望计算出可获得的 bi 分布，使得 S 最小。为此，我们尽快在最大成本边上进行切割，这将达到最佳的 S。如果我们遇到几条具有相同成本的边，我们可以先移除或切割其中任何一条。
C++ 程序
以下是实现上述方法的解决方案，我们首先按降序对边切割成本进行排序，然后从较高成本到较低成本循环遍历它们，构建我们的解决方案。每次我们选择一条边，对应的计数都会增加 1，这将每次乘以相应的边切割成本。
示例
// C++ program to divide a board into p*q squares
#include <bits/stdc++.h>
using namespace std;
int minimumCostOfBreaking(int X1[], int Y1[], int p, int q){
int res1 = 0;
sort(X1, X1 + p, greater<int>());
sort(Y1, Y1 + q, greater<int>());
int hzntl = 1, vert = 1;
int i = 0, j = 0;
while (i < p && j < q){
if (X1[i] > Y1[j]){
res1 += X1[i] * vert;
hzntl++;
i++;
}
else{
res1 += Y1[j] * hzntl;
vert++;
j++;
}
}
int total = 0;
while (i < p)
total += X1[i++];
res1 += total * vert;
total = 0;
while (j < q)
total += Y1[j++];
res1 += total * hzntl;
return res1;
}
int main(){
int p = 6, q = 4;
int X1[p-1] = {3, 2, 4, 2, 5};
int Y1[q-1] = {5, 2, 3};
cout << minimumCostOfBreaking(X1, Y1, p-1, q-1);
return 0;
}输出
65
更新于： 2020-07-23
288 次浏览
广告