闵可夫斯基空间

---

引言

一般来说，我们处理的是三个空间维度，这与我们日常的宏观生活密切相关。然而，根据爱因斯坦的相对论，时间坐标在我们的日常生活中也起作用。这一事实是由科学家赫尔曼·闵可夫斯基提出并证明的。然而，这一概念的诞生源于庞加莱在1905年提出的实验，但当时它还处于简略或原始的形式。后来，在1908年，赫尔曼·闵可夫斯基解释了这个概念。

他将闵可夫斯基空间描述为一个具有四个维度且满足相对论假设的虚空间。这个概念是相对论的数学形式。

什么是闵可夫斯基空间？

当我们谈论空间时，我们会想到它的维度。我们都非常了解空间的三个维度。这里，闵可夫斯基空间这个术语是赫尔曼·闵可夫斯基在研究狭义相对论时提出的一个新概念。他分析了狭义相对论可以在四维空间中更好地解释，并解释了时空维度的概念。根据科学家的姓氏，这个空间被称为闵可夫斯基空间。

根据定义，我们可以说闵可夫斯基空间是一个四维扩展，它具有三个空间维度和一个时间维度。它是数学物理学中的一个概念，用于解释爱因斯坦的相对论。当我们推导出闵可夫斯基空间时，我们发现结果等于相对论的一个假设。时空具有四个维度，但它对时间维度的处理方式与其他三个维度不同；这就是它与所有参考系都一致的原因。闵可夫斯基空间的度规签名表示为(− +++)。闵可夫斯基空间的性质或结构是平坦的，这意味着这个空间像书页一样平坦。

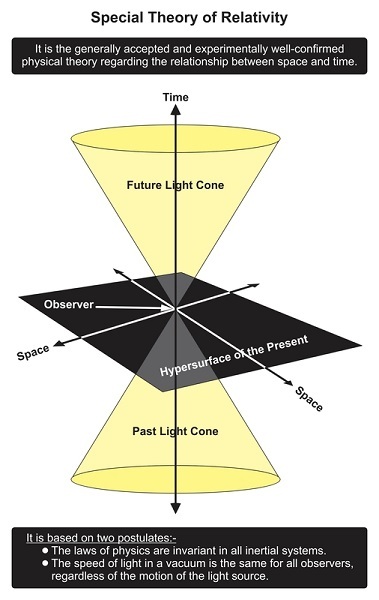
闵可夫斯基时空几何

时空几何是由一位名叫赫尔曼·闵可夫斯基的科学家提出的。他为麦克斯韦电磁方程组发展了这种几何。他发现，如果我们取两个事件，它们之间的时空间隔不会影响惯性参考系。

这种几何是爱因斯坦相对论的一个特殊假设。由于这种时空几何具有四个维度，它们与四个坐标相关联，可以表示为x、y、z和ct。

在数学形式中，我们可以表示所有四个坐标，例如

$$\mathrm{(x_{1},x_{2},x_{3},x_{4})}$$

这里，我们使用第四维度与其他三个维度相同的单位。因此，时间坐标取为光速乘以单位时间或ct。

因此，如果我们测量时空平面中弧线的微分长度，我们得到：

$$\mathrm{\partial\:s^{2}\:=\:\partial\:x^{2}\:\:+\:\partial\:y^{2}\:\:+\:\partial\:z^{2}\:-\:c^{2}\:\partial\:t^{2}}$$

该理论指出时空是平坦的，我们可以用上述方程以如下方式证明这一点：

$$\mathrm{G_{uv}\:=\:[-\:1\:0\:0\:0\:0\:1\:0\:0\:0\:0\:1\:0\:0\:0\:0\:1]}$$

交互式闵可夫斯基图

如果我们想知道以不同速度运动的任何两个物体之间的关系，交互式闵可夫斯基图非常重要。该图向我们提供了时空坐标中相对论的影响。

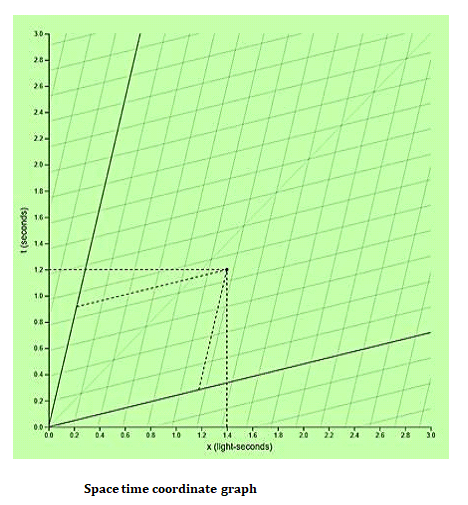
该图具有不同颜色和形状的不同线。该图还有一个红点。每条线和点都有其功能和值。让我们简要了解一下这些线和点。

• 黑线表示静止物体的坐标轴(𝑥, 𝑡)。

• 蓝线表示另一个正在运动的物体的位 置，第二个物体相对于静止物体的速度为v。这里，速度v不等于光速，而是光速的一小部分。

• 这里，只有一个红点表示的点，即在特定时间瞬间发生某事的点。但重要的是要注意，红点在静止物体的坐标(𝑥𝑎𝑡𝑎)处，而同一点在第二个物体的坐标(𝑥′𝑎𝑡′𝑎)处。借助虚线可以观察到这种测量差异。

• 黄线表示光线遵循的路径。

使用闵可夫斯基图和相对论方程，我们可以找到原点和事件发生点之间的路径。

闵可夫斯基空间的重要性

就相对论而言，闵可夫斯基空间非常有用且重要。这个闵可夫斯基空间非常有助于在坐标系中表示洛伦兹变换。

闵可夫斯基图也很有用，因为它对所有坐标系使用单一世界线。我们大多处理的是一对坐标，因此两个坐标都有单一世界线。

结论

本教程完全基于闵可夫斯基空间。在这里，我们了解了揭示闵可夫斯基空间发现原因和结果的事实。此外，我们还了解了相对论是如何运作的，以及时间坐标对对每个人都普遍存在的事件的影响。此外，我们还了解了具有四个维度且平坦的空间。

常见问题

1. 相对论说明了什么？

相对论陈述了一些重要的论点。

• 物理定律对于属于任何惯性参考系的每个观察者都是相同的。

• 真空中光速对于每个人都是相同且相等的。

• 时钟的速度受重力影响，当它处于引力井中时会变慢。

• 光线也受到重力影响。

• 宇宙正在以大于光速的速度持续膨胀。

2. 谁提出了相对论？

相对论是由阿尔伯特·爱因斯坦提出的。

3. 参考系是什么意思？

简单来说，我们可以说参考系是一组位置坐标，我们用它来测量任何运动或静止物体的速度或位移。

4. 惯性参考系和非惯性参考系有什么区别？

在惯性参考系中，牛顿定律适用，而在非惯性参考系中，牛顿运动定律不适用。

5. 什么是洛伦兹变换？

洛伦兹变换是一个定义两组坐标系之间关系的方程。这里，两者都以恒定速度运动。此外，这两个坐标系是相对的。