样本空间

---

介绍

在日常生活中，我们遇到各种具有多种结果的活动。虽然我们无法预测确切的结果，但我们可以估计该事件或活动的所有可能结果。在本教程中，我们将讨论样本空间、一些特殊事件及其可能的结果，并附带解题示例。

样本空间

样本空间是概率论的一个概念，它是随机事件或实验所有可能结果的集合。样本空间用集合符号表示，通常用 S 表示。此外，它也可以用 U（全集）或 𝛺 表示。样本空间包含数字、单词、字母或符号。

同时抛掷 n 枚硬币的样本空间，n = 2, 3, 4, 5

一枚硬币有两面，即正面和反面。让我们将正面表示为“H”，反面表示为“T”。

同时抛掷两枚硬币 -

同时抛掷两枚硬币的可能结果如下 $\mathrm{S\:=\:\lbrace\:(H\:,\:H)\:,\:(H\:,\:T)\:,\:(T\:,\:H)\:,\:(T\:,\:T)\:\rbrace\:}$

$\mathrm{结果数\:=\:4(2^{2})\:(如图所示)}$.

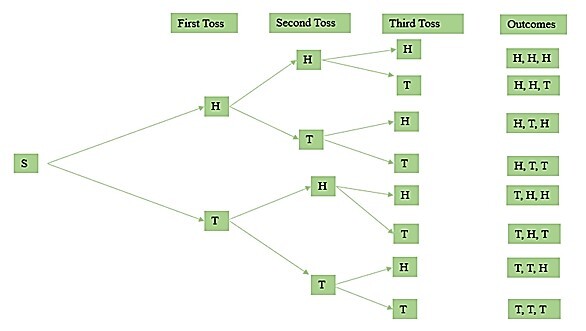
同时抛掷三枚硬币 -

同时抛掷三枚硬币的可能结果如下。

$\mathrm{S\:=\:\lbrace\:(H\:,\:H\:,\:H)\:,\:(H\:,\:H\:,\:T)\:,\:(H\:,\:T\:,\:H)\:,\:(H\:,\:T\:,\:T)\:,\:(T\:,\:H\:,\:H)\:,\:(T\:,\:H\:,\:T)\:,\:(T\:,\:T\:,\:H)\:,\:(T\:,\:T\:,\:T)\rbrace}$

$\mathrm{结果数\:=\:8(2^{3})}$

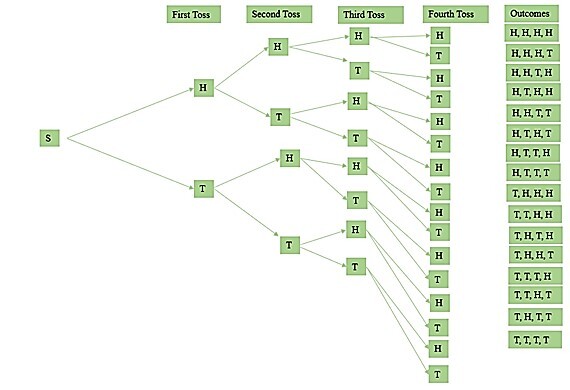
同时抛掷四枚硬币 -

同时抛掷四枚硬币的可能结果如下。

$\mathrm{(H\:,\:H\:,\:H\:,\:H)\:,\:(H\:,\:H\:,\:H\:,\:T)\:,\:(H\:,\:H\:,\:T\:,\:H),(H\:,\:H\:,\:T\:,\:T)\:,\:(H\:,\:T\:,\:H\:,\:H)\:,\:(H\:,\:T\:,\:H\:,\:T)\:,\:(H\:,\:T\:,\:T\:,\:T)\:,\:(H\:,\:H\:,\:T\:,\:T)\:,\:(T\:,\:H\:,\:H\:,\:H)\:,\:(T\:,\:T\:,\:H\:,\:H)\:,\:(T\:,\:H\:,\:T\:,\:H)\:,\:(T\:,\:H\:,\:H\:,\:T)\:,\:(T\:,\:T\:,\:T\:,\:H)\:,\:(T\:,\:T\:,\:H\:,\:T)\:,\:(T\:,\:H\:,\:T\:,\:T)\:,\:(T\:,\:T\:,\:T\:,\:T)}$

$\mathrm{结果数\:=\:16(2^{4})}$

同时抛掷五枚硬币 -

同时抛掷五枚硬币的可能结果如下。

$\mathrm{\lbrace\:(H\:,\:H\:,\:H\:,\:H\:,\:H)\:,\:(H\:,\:H\:,\:H\:,\:H\:,\:T)\:,\:(H\:,\:H\:,\:H\:,\:T\:,\:T)\:,\:(H\:,\:H\:,\:T\:,\:T\:,\:T)\:,\:(H\:,\:T\:,\:T\:,\:T\:,\:T)\:,\:(T\:,\:T\:,\:T\:,\:T\:,\:T)\:,\:(T\:,\:T\:,\:T\:,\:T\:,\:H)\:,\:(T\:,\:T\:,\:T\:,\:H\:,\:H)\:,\:(T\:,\:T\:,\:H\:,\:H\:,\:H)\:,\:(T\:,\:H\:,\:H\:,\:H)\:,\:(H\:,\:T\:,\:H\:,\:T\:,\:H)\:,\:(T\:,\:H\:,\:T\:,\:H\:,\:T)\:,\:(H\:,\:H\:,\:T\:,\:H\:,\:H)\:,\:(T\:,\:T\:,\:H\:,\:T\:,\:T)\:,\:(H\:,\:T\:,\:T\:,\:H\:,\:T)\:,\:(T\:,\:H\:,\:H\:,\:T\:,\:H)\:,\:(T\:,\:H\:,\:H\:,\:H\:,\:T)\:,\:(H\:,\:T\:,\:T\:,\:T\:,\:H)\:,\:(T\:,\:H\:,\:H\:,\:T\:,\:T)\:,\:(H\:,\:T\:,\:T\:,\:H\:,\:H)\:,\:(H\:,\:H\:,\:T\:,\:T\:,\:H)\:,\:(T\:,\:T\:,\:H\:,\:H\:,\:T)\:,\:(T\:,\:T\:,\:H\:,\:T\:,\:H)\:,\:(H\:,\:H\:,\:T\:,\:H\:,\:T)\:,\:(H\:,\:T\:,\:H\:,\:T\:,\:T)\:,\:(T\:,\:H\:,\:T\:,\:H\:,\:H)\:,\:(T\:,\:H\:,\:T\:,\:H\:,\:H)\:,\:(T\:,\:H\:,\:T\:,\:T\:,\:H)\:,\:(H\:,\:T\:,\:H\:,\:H\:,\:T)\:,\:(H\:,\:T\:,\:H\:,\:T\:,\:T)\:,\:(T\:,\:H\:,\:T\:,\:H\:,\:H)\:,\:(H\:,\:H\:,\:H\:,\:T\:,\:H)\:,\:(T, T\:,\:T\:,\:H\:,\:T)\:\rbrace }$

$\mathrm{结果数\:=\:32(2^{5})}$

同时抛掷 2 个骰子的样本空间

如果同时抛掷两个骰子，我们将得到 36 个结果，如下所示 -

$\mathrm{S\:=\:\lbrace\:(1\:,\:1)\:,\:(1\:,\:2)\:,\:(1\:,\:3)\:,\:(1\:,\:4)\:,\:(1\:,\:5)\:,\:(1\:,\:6)\:,\:(2\:,\:1)\:,\:(2\:,\:2)\:,\:(2\:,\:3)\:,\:(2\:,\:4)\:,\:(2\:,\:5)\:,\:(2\:,\:6)\:,\:(3\:,\:1)\:,\:(3\:,\:2)\:,\:(3\:,\:3)\:,\:(3\:,\:4)\:,\:(3\:,\:5)\:,\:(3\:,\:6)\:,\:(4\:,\:1)\:,\:(4, 2)\:,\:(4\:,\:3)\:,\:(4\:,\:4)\:,\:(4\:,\:5)\:,\:(4\:,\:6)\:,\:(5,1)\:,\:(5\:,\:2)\:,\:(5\:,\:3)\:,\:(5\:,\:4)\:,\:(5\:,\:5)\:,\:(5\:,\:6)\:,\:(6\:,\:1)\:,\:(6\:,\:2)\:,\:(6\:,\:3)\:,\:(6\:,\:4)\:,\:(6\:,\:5)\:,\:(6\:,\:6)\rbrace\:.}$

同时抛掷 1、2、3 枚硬币和 1 个骰子的样本空间

让我们考虑抛掷一枚硬币和一个骰子的事件。可能的结果将是

$\mathrm{S\:=\:\lbrace\:(H\:,\:1)\:,\:(2\:,\:H)\:,\:(3\:,\:H)\:,\:(4\:,\:H)\:,\:(5\:,\:H)\:,\:(6\:,\:H)\:,\:(1\:,\:T)\:,\:(2\:,\:T)\:,\:(3\:,\:T)\:,\:(4\:,\:T)\:,\:(5\:,\:T)\:,\:(6, H)\:\rbrace\:.}$

$\mathrm{结果总数\:=\:2\:\times\:6\:=\:12}$

让我们考虑抛掷两枚硬币和一个骰子的事件。可能的结果将是

$\mathrm{S\:=\:\lbrace\:(H\:,\:H\:,\:1)\:,\:(H\:,\:H\:,\:2)\:,\:(H\:,\:H\:,\:3)\:,\:(H\:,\:H\:,\:4)\:,\:(H\:,\:H\:,\:5)\:,\:(H\:,\:H\:,\:6)\:,\:(T\:,\:T\:,\:1)\:,\:(T\:,\:T\:,\:2)\:,\:(T\:,\:T\:,\:3)\:,\:(T\:,\:T\:,\:4)\:,\:(T\:,\:T\:,\:5)\:,\:(T\:,\:T\:,\:6)\:,\:(T\:,\:H\:,\:1)\:,\:(T\:,\:H\:,\:2)\:,\:(T\:,\:H\:,\:3)\:,\:(T\:,\:H\:,\:4)\:,\:(T\:,\:H\:,\:5)\:,\:(T\:,\:H\:,\:6)\:,\:(H\:,\:T\:,\:1)\:,\:(H\:,\:T\:,\:2)\:,\:(H\:,\:T\:,\:3)\:,\:(H\:,\:T\:,\:4)\:,\:(H\:,\:T\:,\:5)\:,\:(H\:,\:T\:,\:6)\rbrace\:.}$

$\mathrm{结果总数\:=\:2\times\:2\times\:6\:=\:24}$

让我们考虑抛掷三枚硬币和一个骰子的事件

$\mathrm{结果总数\:=\:2\times\:2\times\:2\times\:6\:=\:48}$

$\mathrm{S\:=\:\lbrace\:(H\:,\:H\:,\:H\:,\:1)\:,\:(H\:,\:H\:,\:H\:,\:2)\:,\:(H\:,\:H\:,\:H\:,\:3)\:,\:(H\:,\:H\:,\:H\:,\:4)\:,\:(H\:,\:H\:,\:H\:,\:5)\:,\:(H\:,\:H\:,\:H\:,\:6)\:,\:(H\:,\:H\:,\:T\:,\:1)\:,\:(H\:,\:H\:,\:T\:,\:2)\:,\:(H\:,\:H\:,\:T\:,\:3)\:,\:(H\:,\:H\:,\:T\:,\:4)\:,\:(H\:,\:H\:,\:T\:,\:5)\:,\:(H\:,\:H\:,\:T\:,\:6)\:,\:(H\:,\:T\:,\:H\:,\:1)\:,\:(H\:,\:T\:,\:H\:,\:2)\:,\:(H\:,\:T\:,\:H\:,\:3)\:,\:(H\:,\:T\:,\:H\:,\:4)\:,\:(H\:,\:T\:,\:H\:,\:5)\:,\:(H\:,\:T\:,\:H\:,\:6)\:,\:(H\:,\:T\:,\:T\:,\:1)\:,\:(H\:,\:T\:,\:T\:,\:2)\:,\:(H\:,\:T\:,\:T\:,\:3)\:,\:(H\:,\:T\:,\:T\:,\:4)\:,\:(H\:,\:T\:,\:T\:,\:5)\:,\:(H\:,\:H\:,\:T\:,\:6)\:,\:(T\:,\:H\:,\:H\:,\:1)\:,\:(T\:,\:H\:,\:H\:,\:2)\:,\:(T\:,\:H\:,\:H\:,\:3)\:,\:(T\:,\:H\:,\:H\:,\:4)\:,\:(T\:,\:H\:,\:H\:,\:5)\:,\:(T\:,\:H\:,\:H\:,\:6)\:,\:(T\:,\:H\:,\:T\:,\:1)\:,\:(T\:,\:H\:,\:T\:,\:2)\:,\:(T\:,\:H\:,\:T\:,\:3)\:,\:(T\:,\:H\:,\:T\:,\:4)\:,\:(T\:,\:H\:,\:T\:,\:5)\:,\:(T\:,\:H\:,\:T\:,\:6)\:,\:(T\:,\:T\:,\:H\:,\:1)\:,\:(T\:,\:T\:,\:H\:,\:2)\:,\:(T\:,\:T\:,\:H\:,\:3)\:,\:(T\:,\:T\:,\:H\:,\:4)\:,\:(T\:,\:T\:,\:H\:,\:5)\:,\:(T\:,\:T\:,\:H\:,\:6)\:,\:(T\:,\:T\:,\:T\:,\:1)\:,\:(T\:,\:T\:,\:T\:,\:2)\:,\:(T\:,\:T\:,\:T\:,\:3)\:,\:(T\:,\:T\:,\:T\:,\:4)\:,\:(T\:,\:T\:,\:T\:,\:5)\:,\:(T\:,\:T\:,\:T\:,\:6)\:\rbrace\:}$

事件

事件定义为样本空间的子集。事件是在试验中发生的特定事件。例如，抛硬币时得到正面是一个事件的例子。

$\mathrm{事件\:=\:E\:=\:\lbrace\:\:\rbrace\:}$

$\mathrm{S\:=\:\lbrace\:所有可能的结果\:\rbrace\:}$

概率

在数学中，概率被定义为对事件发生可能性进行的数值描述。换句话说，它说明了事件发生的可能性。概率的数值介于 0 和 1 之间。概率值越高，事件发生的可能性就越大。概率的概念广泛应用于科学、金融、人工智能、博弈论、计算机科学等领域。

解题示例

示例 1

抛硬币时，正面和反面的概率是多少？

解答 -

$\mathrm{正面概率\:=\:\frac{1}{2}}$

$\mathrm{反面概率\:=\:\frac{1}{2}}$

示例 2

给定区间 [1, 12] 的样本空间是什么？

解答 -

由于该区间是闭区间，因此数字 1 和 12 也包含在样本空间中。

因此，样本空间为 $\mathrm{=\:S\:=\:\lbrace\:1\:,\:2\:,\:3\:,\:4\:,\:5\:,\:6\:,\:7\:,\:8\:,\:9\:,\:10\:,\:11\:,\:12\:\rbrace\:}$

结论

本文简要介绍了样本空间。描述了事件和样本空间之间的基本区别，并附带各种示例。此外，还确定了各种知名事件的样本空间。总之，本文可能有助于理解样本空间的基本概念。

常见问题

1. 如果一个骰子抛掷三次，结果数是多少？

如果一个骰子抛掷三次，结果数为 $\mathrm{=\:6\:\times\:6\:\times\:6\:=\:216}$.

2. 概率有哪些应用？

概率的概念广泛应用于科学、金融、人工智能、博弈论、计算机科学等领域。

3. 表示样本空间的可能方法有哪些？

样本空间可以用三种方式表示为

• 表格形式

• 列表形式

• 树状图

4. 概率值可以大于 1 吗？

不可以，因为概率的最大值为 1。因此，它总是小于 1。

5. 如果一枚硬币抛掷 6 次，结果数是多少？

如果一枚硬币抛掷 6 次，结果数为 $\mathrm{2^{6}\:=\:64}$.