八边形

---

简介

• 多边形是在二维空间中具有有限数量边的几何图形。

• 八边形是一个八边的多边形。

• 所有边都相等的多边形称为正八边形。

• 八边形有八个内角，根据边长的不同，内角的大小也各不相同。

• 根据边长和内角的不同，八边形有不同的类型。

• 八边形共有20 条对角线。

多边形

• 多边形是由连接有限数量线段形成的二维图形。

• 这些线段称为边，边的数量决定了多边形的不同形状。

• 构成多边形至少需要三条边。

• 两条不同线段的交点称为顶点，在顶点处形成多边形的内角。

• 不同的角度和边长构成了不同类型的多边形，例如正多边形、非正多边形、凸多边形和凹多边形。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

多边形的不同形状

• 三角形是三边形

• 四边形是四边形

• 五边形是五边形

• 六边形是六边形

• 七边形是七边形

• 八边形是八边形

类似地，九边形称为九边形，十边形称为十边形。

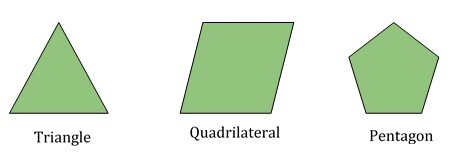
以上三个图形分别表示三角形、四边形和五边形。

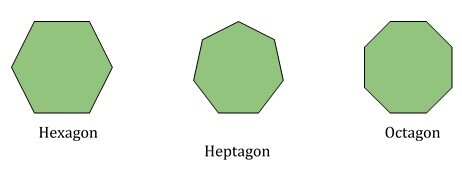
以下三个图形分别表示六边形、七边形和八边形。

多边形的类型

• 正多边形 - 如果多边形所有边长相等且所有角都具有相同的度数，则该多边形为正多边形。

• 非正多边形 - 如果多边形边长不相等且角也不相等，则该多边形为非正多边形。

• 凸多边形 - 如果多边形的所有内角都小于 180 度，则它是一个凸多边形。

• 凹多边形 - 如果多边形中至少有一个内角大于 180 度，则它是一个凹多边形。

多边形的性质

n 边形的所有内角之和等于 $\mathrm{(n-2)\times 180^o}$。

在 n 边形中，对角线的数量等于 $\mathrm{\frac{n\times (n-3)}{2}}$

在 n 边正多边形中，每个内角都等于 $\mathrm{\frac{(n-2)×180^o}{n}}$

在 n 边正多边形中，每个外角都等于 $\mathrm{\frac{360^o}{n}}$

八边形

八边形是八边形。它有八条边、八个顶点、八个内角和八个外角。

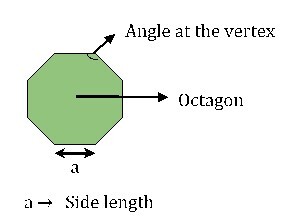
下图是一个边长为 'a' 的正八边形。

八边形 (n=8) 中所有内角之和等于 $\mathrm{(n-2)×180^o=1080^o}$

八边形的类型

• 正八边形 - 如果八边形所有边长相等且所有角都具有相同的度数，则该八边形为正八边形。

• 非正八边形 - 如果八边形边长不相等且角也不相等，则该八边形为非正八边形。

• 凸八边形 - 如果八边形的所有内角都小于 180 度，则它是一个凸八边形。

• 凹八边形 - 如果八边形中至少有一个内角大于 180 度，则它是一个凹八边形。

八边形的性质

• 正八边形中所有内角的度数为：n = 8

  $$\mathrm{\frac{(n-2)×180^o}{n}=\frac{(8-2)×180^o}{8} = 135\: 度. }$$

• 正八边形中所有外角的度数为：n = 8

  $$\mathrm{\frac{360^o}{n}=\frac{360^o}{8}= 45\: 度.}$$

• 八边形中的对角线条数为：n = 8

  $$\mathrm{\frac{n×(n-3)}{2}=\frac{8×(8-3)}{2}=20}$$

• 八边形的周长等于所有边长的总和。在边长为'a'的正八边形中，周长等于 8a。

• 在边长为 'a' 的正八边形中，正八边形的面积等于 $\mathrm{2×a^2×(1+\sqrt{2}).}$

• 所有正八边形都是凸八边形，因为所有角都等于 135 度，小于 180 度，而非正八边形可以是凸八边形或凹八边形。

• 连接任何两个相对顶点可以形成八边形的最长对角线，在边长为 'a' 的正八边形中，最长对角线的长度为：$\mathrm{a×\sqrt{4+2×\sqrt{2}}}$

八边形的对称轴

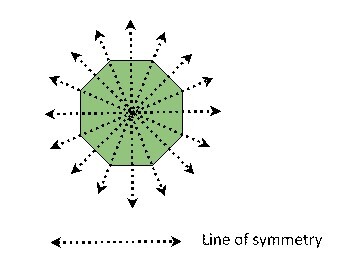
如果一条线将多边形分成两半，则称为对称轴。在正八边形中，可能有八条对称轴。下图是一个具有八条对称轴的正多边形。

现实生活中的八边形

八边形二维图形在现实生活中有多种用途，例如交通指示牌中的开始和停止标志为八边形。还有各种模拟壁钟为八边形。从上方看，雨伞也是八边形。

例题

1) 求一个八边形的周长，其边长分别为 2、3、4、5、6、7、8 和 9？所有边长单位为厘米。

八边形的周长等于其所有边长的总和。

周长 = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 44

八边形的周长等于 44 厘米。

2) 如果所有边长都等于 3 厘米，则求八边形的面积？

边长为 'a' 的正八边形的面积等于 2×a²×(1+\sqrt{2})

a = 3；面积 =2×a²×(1+\sqrt{2}) =2×3²×(1+\sqrt{2})=43.45

八边形的面积 = 43.45 平方厘米

3) 边长等于 4 厘米的正多边形的最长对角线的长度是多少？

边长为 'a' 的正八边形的最长对角线的长度为：$\mathrm{a×\sqrt{4+2×\sqrt{2}}}$

已知 a = 4

最长对角线的长度 =$\mathrm{a×\sqrt{4+2×\sqrt{2}}=4×\sqrt{4+2×\sqrt{2}}=10.4\: 厘米 }$

最长对角线的长度 = 10.4 厘米

结论

在本教程中，我们学习了多边形、多边形的类型、多边形的一些性质、八边形、八边形的性质、八边形的对称轴以及现实生活中的八边形。

常见问题

1.七边形有多少条边？

七边形是七边形。因此，七边形有七条边。

2.如何求多边形的对角线条数？

在 n 边形中，对角线的数量等于 $\mathrm{\frac{n×(n-3)}{2}}$

3.正八边形可能有多少条对称轴？

在正八边形中，可能有八条对称轴。

4.八边形的所有内角之和是多少？

八边形 (n=8) 中所有内角之和等于 $\mathrm{(n-2)×180^o=1080^o}$

5.凸八边形是什么意思？

如果八边形的所有内角都小于 180 度，则它是一个凸八边形。