一个边长为4米的正方形，在其四个角处切去部分形成一个等边八边形。求八边形的边长（单位：米）。

已知

一个边长为4米的正方形，在其四个角处切去部分形成一个等边八边形。

要求

求八边形的边长。

解答

设切去的每个角的边长为$2x$米。

这意味着：

所形成的八边形的边长为$(4-x-x)$米$=(4-2x)$米。

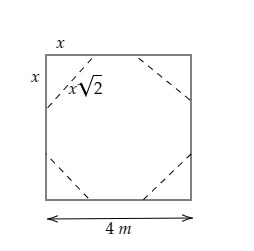
从图中可以看出：

八边形的边长为$\sqrt{x^2+x^2}=x\sqrt{2}$。

因此：

$4-2x=x\sqrt2$

$4=x\sqrt2+2x$

$4=x(\sqrt2+2)$

$x=\frac{4}{2+\sqrt2}$

$x=\frac{4}{3.4}$

$x=1.17$

八边形的边长$=1.17\times1.41=1.65$米

八边形的每条边长为1.65米。

Tutorialspoint

更新于：2022年10月10日

224次浏览

开启你的职业生涯

完成课程获得认证

开始学习