数轴上的整数运算

---

简介

整数的运算，例如加法、减法、乘法和除法，可以在数轴系统中解释。在日常生活中，我们需要对数字进行各种代数运算。数学中使用了各种类型的数字。具体来说，整数是一种广泛使用的特殊类型的数字。整数的表示和一些数学运算都是必要的。在本教程中，我们将学习数系、整数、它们在数轴上的表示、数轴上整数的比较和运算，并提供一些已解决的示例。

数系

数字是一个数学术语，它具有一定的值，用于计数或测量物体。数学中包含各种数字，例如自然数、整数、有理数和无理数。然而，数系被定义为以计算机可以理解的各种形式表示数字。数系也被称为记数系统。代数中有四种类型的数系，例如

• 十进制 (基数-10) − 在此系统中，总共有 10 个数字，即 0、1、2、3、4、5、6、7、8 和 9

• 二进制 (基数-2) − 它只使用两个数字，例如 0 和 1，来表示任何数字

• 八进制 (基数-8) − 它使用 8 个数字，例如 0、1、2、3、4、5、6 和 7，来表示任何数字。

• 十六进制 (基数-16) − 它使用 16 个数字或字母，包括 0、1、2、3、4、5、6、7、8、9 和 A、B、C、D、E、F。

整数

数字的集合包含整数和负数，但不包含分数或比率项。也就是说，… -4、-3、-2、-1、0、1、2、3、4… 称为整数。整数分为 3 种类型。

• 正整数 − 如果整数的值大于零，则称为正整数。例如，4、76、5、9、34 等。

• 负整数 − 如果整数的值小于零，则称为负整数。例如，-8、-10、-16、-100、-4 等。

• 零 − 数字“0”既不是正整数也不是负整数。但是，它是一个整数。

整数的数轴

数轴是一条用整数标记的刻度直线。初等数学中有两种类型的数轴，例如水平整数和垂直整数。数轴上的数字等距。下面给出了数轴的示例。

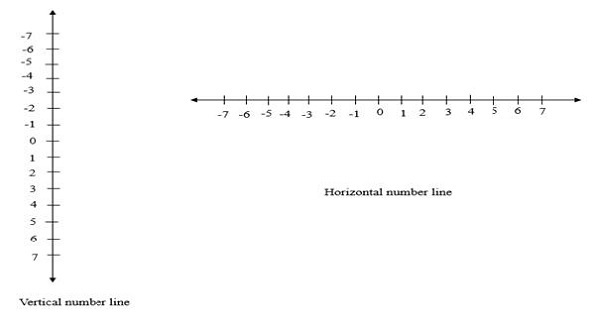
它也用于执行整数之间的比较分析和代数运算。数轴有四个部分。

• 中心部分 − 0 是数轴的原点或中心部分。

• 左部分 − 数轴的左部分表示负整数

• 右部分 − 数轴的右部分表示正整数。

数轴上整数的表示

数轴有四个部分。

• 中心部分 − 0 是数轴的原点或中心部分。

• 左部分 − 数轴的左部分表示负整数。

• 右部分 − 数轴的右部分表示正整数。

假设我们必须表示数字 4。然后，我们必须向零的右侧移动 4 个点。

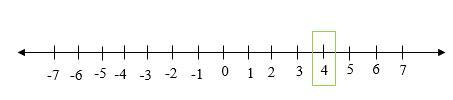
假设我们必须表示数字 -6。然后，我们必须向零的左侧移动 6 个点。

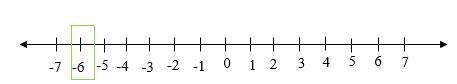
数轴上整数的比较

数轴可用于比较两个整数。在比较两个整数时，位于右侧较远的整数较大。同样，位于左侧较远的整数较小。

例如，我们必须比较 -3 和 8。由于整数“8”比“-3”更靠右，因此 8 大于 -3。它也可以写成 8 > 3。

同样，比较 0 和 -4。由于整数“-4”比“0”更靠左，因此 -4 小于 0。它也可以写成 -4 < 0 或 0 > -4。

使用数轴进行整数运算

四种基本的代数运算，例如整数的加法、减法、乘法和除法，可以在数轴系统中解释。

整数的加法

数轴上整数的加法可以通过观察第二个整数的符号来执行。如果第二个整数为正，我们将向右移动，否则我们将向左移动。

让我们考虑一个例子。使用数轴将 4 和 -3 相加。应遵循以下步骤来找到上述整数的和。

• 在数轴上标记第一个整数，即 4。

• 现在，从第一个数字开始，向左移动与第二个数字相同的单位。

• $\mathrm{4\:+\:(-3)\:=\:1}$

整数的减法

数轴上整数的减法可以通过观察第二个整数的符号来执行。如果第二个整数为正，我们将向左移动，或者向右移动。

让我们考虑一个例子。使用数轴从 -1 中减去 -4。应遵循以下步骤来找到上述整数的差。

• 在数轴上标记第一个整数，即 -1。

• 现在，从第一个数字开始，向右移动与第二个数字相同的单位。

• $\mathrm{-1\:-\:(-4)\:=\:3}$

整数的乘法

两个整数的乘法可以通过以下步骤完成。

• 从零开始，用第一个数字计数，次数由第二个数字指示。

整数乘法有一些规则。

$\mathrm{正数\:\times\:正数}$	正数
$\mathrm{负数\:\times\:正数}$	负数
$\mathrm{正数\:\times\:负数}$	负数
$\mathrm{负数\:\times\:负数}$	正数

整数的除法

两个整数的除法可以通过以下步骤完成。

• 在数轴上选择从零开始的确定线段。

• 将此线段均匀地分成由第二个整数指示的部分。

• 每个部分的长度将是除法的结果。

已解决的示例

1) 使用数轴从 -2 中减去 6。

答案 - 根据问题，我们必须找到 -2 - (6) 的结果。

应遵循以下步骤来找到上述整数的差。

• 在数轴上标记第一个整数，即 -2。

• 由于第二个整数是正数，因此，从第一个数字开始，向左移动与第二个数字相同的单位。

• $\mathrm{-2\:-\:(6)\:=\:-8}$

2) 将 2 和 -4 相乘。

答案 - 应遵循以下步骤来找到上述整数的积。

• 以 0 为参考。

• 以 2 为单位计数四次，得到 8 的结果。

• 由于 $\mathrm{正数\:\times\:负数\:=\:负数}$，因此结果将为 -8

结论

本教程简要介绍了整数和数轴的基本概念。本教程描述了数系、整数和数轴的基本定义。此外，还使用数轴描述了整数的表示及其基本运算。此外，还提供了一些已解决的示例，以便更好地理解此概念。总之，本教程可能有助于理解数轴上整数运算的基本概念。

常见问题解答

1. 两个负整数相除的结果是多少？

负整数相除的结果始终为正整数

2. 哪些数字可以在数轴上表示？

数轴可用于表示自然数、整数、小数、分数、有理数和无理数。

3. 什么是双数轴？

双数轴是两条平行线，表示等价比率。刻度的位置在两条数轴上匹配。

4. 定义数系的基数？

基数被定义为可用于表示数字的整数。十进制系统中最常用的基数是基数 10。

5. 什么是开放数轴？

如果数轴上没有标记任何数字或整数，则称为开放数轴。它通常用于整数的加法和减法。