一个质量为 1 kg 的物体从 5 米高处落下，得到以下数据

离地高度	速度
$5\ m$	$0\ m/s$
$3.2\ m$	$6\ m/s$
$0\ m$	$10\ m/s$

通过计算说明以上数据是否验证了能量守恒定律（忽略空气阻力）。$(g=10\ m/s^2)$."

物体的给定数据可以如下图所示：

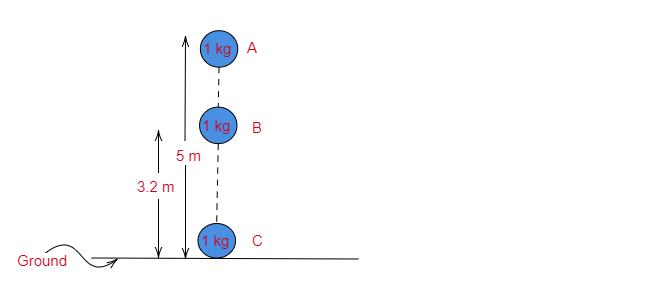 如题，物体质量 $m=1\ kg$

重力加速度 $g=10\ m/s^2$

在 A 点 $(高度=5\ m)$

速度 $v=0$     [如数据表所示]

高度 $h=5\ m$

因此，动能 $K_A=\frac{1}{2}mv^2$

$=\frac{1}{2}\times1\ kg\times 0$

$=0$

其势能 $P_A=mgh$

$=1\ kg\times 10\ m/s^2\times 5\ m$

$=50\ J$

总能量 $E=K_A+P_A$

$=0+50\ J$

$=50\ J$

在 B 点 $(高度=3.2\ m)$：

速度 $v=6\ m/s$

高度 $h=3.2\ m$

因此，动能 $K_B=\frac{1}{2}mv^2$

$=\frac{1}{2}\times1\ kg\times(6\ m/s)^2$

$=18\ J$

其在 B 点的势能，$P_B=mgh$

$=1\ kg\times10\ m/s^2\times3.2\ m$

$=32\ J$

B 点的总能量，$E_B=K_B+P_B$

$=18\ J+32\ J$

$=50\ J$

在 C 点 $(地面，h=0)$

速度 $v_C=10\ m/s$

高度 $h=0$

因此，动能 $K_C=\frac{1}{2}mv^2$

$=\frac{1}{2}\times 1\ kg\times 10^2$

$=50\ J$

势能 $P_C=mgh$

$=1\ kg\times10\ m/s^2\times 0$

$=0$

因此，地面（C 点）的总能量，$E_C=K_C+P_C$

$=50\ J+0$

$=50\ J$

很明显，总能量在每个点都保持不变，这证明了能量守恒定律。

教程点

更新于： 2022年10月10日

77 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习