数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究路径测试和基本路径测试示例
基本路径测试是一种基于程序或模块控制结构的白盒测试技术。使用此结构创建控制流图，并使用此结构测试图中的许多可能路径。
识别控制流图中提供程序或模块的基础执行路径集的路径的方法称为基本路径测试。
由于此测试依赖于程序的控制结构，因此需要深入了解程序的结构。使用此技术创建测试用例遵循四个阶段：
创建控制流图。
计算图的环路复杂度
识别未连接的路径
基于独立路径创建测试用例。
控制流图
控制流图（或简称流图）是一个有向图，它描述了程序或模块的控制结构。控制流图由 V 个节点/顶点和 E 个边组成（V，E）。控制图还可以包含以下内容：
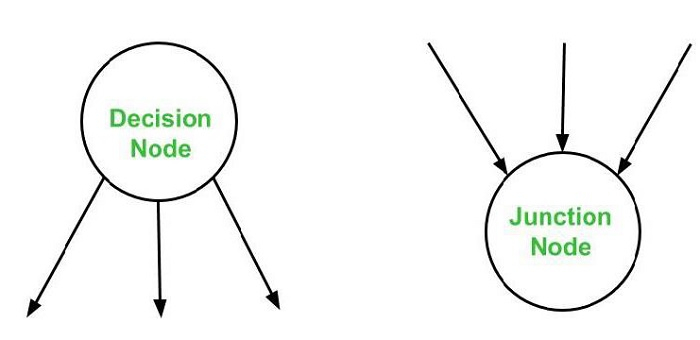
有多个箭头进入的节点称为连接节点。
有多个箭头离开的节点称为决策节点。
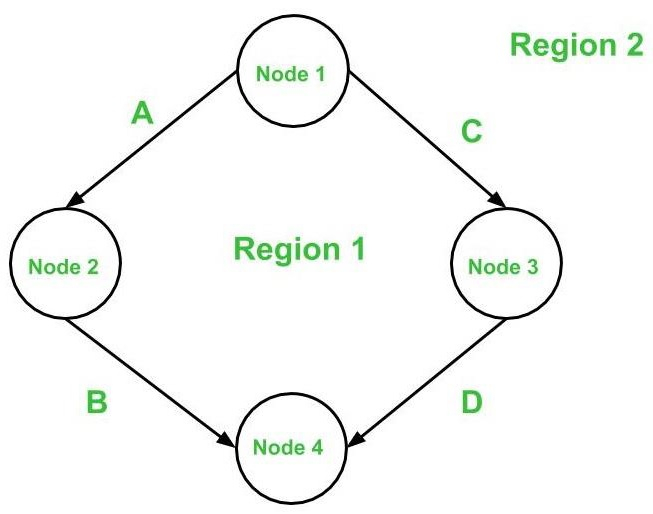
边和节点所包围的区域称为区域（图外部的区域也计为一个区域）。
以下是构建流图时使用的符号：
- 顺序语句：
- 如果 - 则 - 否则
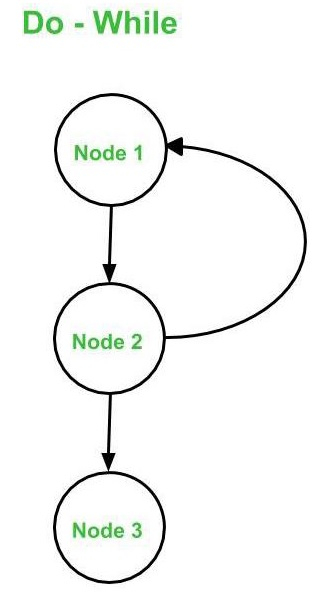
- 执行 - 直到
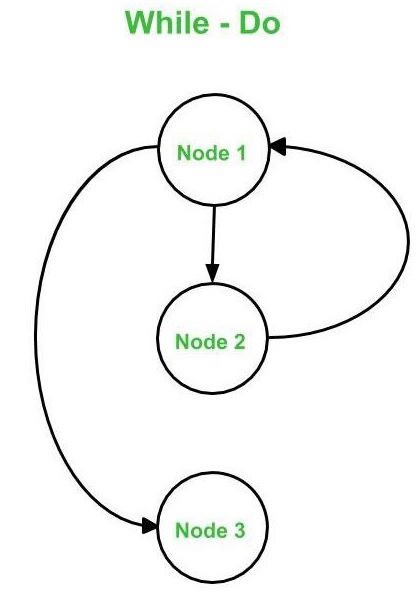
- 当 - 执行
- 开关 - 案例
环路复杂度
环路复杂度 V(G) 被认为是程序逻辑复杂度的度量。可以使用三种不同的公式来计算它：
V(G) = e - n + 2*P 是基于边和节点的公式。
其中 e 是边的数量，n 表示顶点的数量，P 表示连接组件的数量。
例如，请参见上面显示的第一个图。
其中e = 4，n = 4，和p = 1都是整数
V(G) = 4 - 4 + 2 * 1 = 2 环路复杂度
以下是基于决策节点的公式：
V(G) = d + P，其中 d 表示决策节点的数量，P 表示连接节点的数量。
例如，请参见上面显示的第一个图。
其中d=1和p=1
V(G) = 1 + 1 = 2 环路复杂度
以下是基于区域的公式：
V(G) 表示图中区域的数量。
例如，请参见上面显示的第一个图。
V(G) = 1（对于区域 1）+ 1（对于区域 2）= 2 环路复杂度
因此，使用所有三个公式得出的环路复杂度保持不变。这三个公式可用于计算和验证流图的环路复杂度。
观察
每个函数[例如 Main( ) 或 Factorial() ]只创建一个流图。如果程序中有多个函数，则为每个函数创建一个单独的流图。此外，环路复杂度公式中“p”的值由图的总数决定。
如果正好有两个箭头离开决策节点，则将其计为一个决策节点。如果有多于两个箭头离开决策节点，则使用以下公式：
d = k - 1
k 表示离开决策节点的箭头数。
独立路径
在控制流图中，独立路径是指在创建路径之前从未遍历过的至少一条新边的路径。流图的环路复杂度是存在的独立路径的数量。这是因为环路复杂度用作应运行测试次数的上限，以确保程序的所有语句至少运行一次。
在第一个图中，独立路径的数量等于环路复杂度，因此独立路径的数量为 2。
因此，在上面提到的第一个图中，独立路径为：
- A -> B 是第一条路径。
- C 是第二条路径。
注意：值得注意的是，独立路径不一定是唯一的。换句话说，如果图的环路复杂度为 N，则有可能找到两个不同的路径集，每个路径集本质上都是独立的。
最后，一旦获得单独的路径，就可以构造测试用例，每个测试用例表示一个或多个独立路径。
路径测试示例
在之前的文章中，我们研究了使用基本路径测试为程序创建测试用例所涉及的步骤。现在让我们使用相同的步骤解决一个示例。
考虑以下程序，该程序确定一个整数是否为素数。以下是以下程序的时间表：
创建控制流图。
使用所有可用方法计算循环复杂度。
列出所有独立路径设计测试用例。
int main (){
int n, index;
cout << "Enter a number: " << endl;
cin >> n;
index = 2;
while (index <= n - 1) {
if (n % index == 0) {
cout << "It is not a prime number" << endl;
break;
}
index++;
}
if (index == n)
cout << "It is a prime number" << endl;
} // end main解决方案：1. 创建控制流图
步骤 1：在声明变量后，开始对语句进行编号（如果该语句中没有初始化变量）。但是，如果在同一行初始化和声明变量，则应从该行开始编号。
以下是为提供的程序执行编号的方式：
int main (){
int n, index;
cout << "Enter a number: " <> n;
index = 2;
while (index <= n - 1){
if (n % index == 0){
cout << "It is not a prime number" << endl;
break;
}
index++;
}
if (index == n)
cout << "It is a prime number" << endl;
} // end main步骤 2：将所有顺序语句合并到一个节点中。例如，语句 1、2 和 3 都是顺序语句，应连接到一个节点中。对于其余语句，我们将使用此处描述的符号。
注意：为简单起见，按字母顺序对节点进行编号。
生成的图形如下所示：
使用以下公式计算环路复杂度：
方法 1
V(G) = e - n + 2*p
在上图的控制流图中，
其中 e = 10，n = 8，p =1
因此，V(G) = 10 - 8 + 2 * 1 = 4 环路复杂度
方法 2
V(G) = d + p
在上图的控制流图中，
其中 d = 3（节点 B、C 和 F）和 p = 1
因此，环路复杂度 V(G) = 3 + 1 = 4
方法 3
V(G) = 区域数（方法 3）
在上图的控制流图中，有四个区域，如下所示：
因此，有四个不同的区域：R1、R2、R3 和 R4。
V(G) = 1 + 1 + 1 + 1 = 4 环路复杂度
值得注意的是，所有三种方法都获得相同的环路复杂度 V 值 (G)。
独立路径
由于图的环路复杂度 V(G) 为 4，因此有 4 条独立路径。
路径 1 覆盖（红色）以下边：
A – B – F – G – H 是第一条路径。
路径 1 和路径 2 覆盖以下边：
A – B – F – H 是第二条路径。
路径 1、路径 2 和路径 3 覆盖以下边：
A - B - C - E - B - F - G - H 是第三条路径
只有两条边未被覆盖，即边 C-D 和边 D-F。因此，这两条边必须包含在路径 4 中。
A - B - C - D - F - H 是第四条路径。
这些路径中的每条路径都至少有一条以前从未遍历过的新边。
请注意，独立路径并不总是唯一的。
测试用例
我们必须使用先前发现的独立路径来生成测试用例。以这样的方式向程序提供输入，即执行每条独立路径以创建测试用例。
对于提供的程序，将获得以下测试用例：
| 测试用例 ID | 输入数字 | 输出 | 覆盖的独立路径 |
|---|---|---|---|
| 1 | 1 | 无输出 | A-B-F-H |
| 2 | 2 | 它是一个素数 | A-B-F-G-H |
| 3 | 3 | 它是一个素数 | A-B-C-E-B-F-G-H |
| 4 | 4 | 它不是一个素数 | A-B-C-D-F-H |
基本路径测试的优点
基本路径测试在以下情况下很有用：
额外覆盖率：因为它侧重于最大逻辑覆盖率而不是最大路径覆盖率，所以基本路径测试提供了最佳的代码覆盖率。因此，代码总体上得到了很好的测试。
维护测试：当修改软件的一部分时，仍然需要测试所做的更改，这需要路径测试。
当开发人员生成代码时，他或她首先要做的是测试程序或模块的结构。因此，基本路径测试需要深入了解代码的结构。
集成测试：当一个模块调用另一个模块时，存在相当大的接口问题风险。路径测试用于测试模块接口上的所有路径，以避免此类问题。
测试工作量：由于软件（即程序或模块）的环路复杂度是使用基本路径测试技术计算的，因此很明显可以观察到，基本路径测试中的测试工作量与软件或程序的复杂度直接相关。
19K+ 次浏览
