周期函数

---

简介

为了理解波和信号的研究，使用了周期表。在物理学中，人们观察到运动负责在特定时间间隔内返回到相同的值。基于这些特定概念，所有类型的周期运动都被称为周期函数。专注于这些概念，本教程包含了与周期函数相关的信息，以及它的性质和公式。

什么是周期函数？

在过程中，基于固定的时间间隔，重复发生的运动通常称为周期函数。因此，周期函数可以定义为在每个时间单位内恢复到相似值的特定函数（Zafar 等人，2020）。周期函数的周期运动可以分为两种不同的类型：振荡运动和简谐运动。

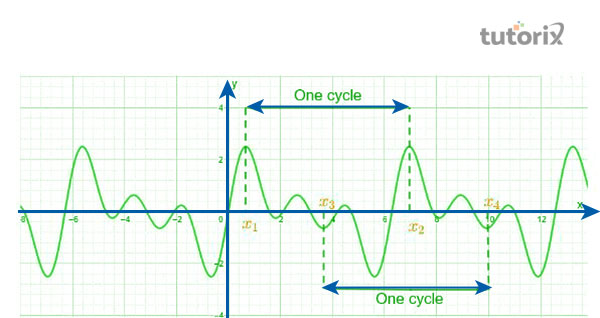
图 1：周期函数

然而，振荡运动和周期运动之间存在差异，因为人们观察到周期运动与任何在一段时间内表现出重复的运动相关。（Analyzemath.com，2022）。

另一方面，振荡运动指的是在两个状态或围绕平衡点执行的运动，如下面的图所示。

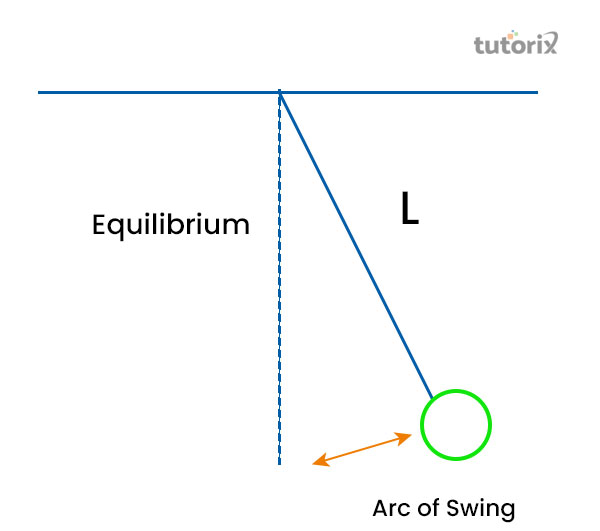
图 2：振荡运动

为了理解这两个不同的概念，需要将摆的运动纳入考虑。摆有一个特定的平衡位置，它会形成一个摆动的弧线，运动使摆来回运动。

周期函数的性质

为了更深入地理解这个概念，需要了解周期函数的性质。

• 第一个需要了解的属性是周期“函数的图形是”对称的”，它沿水平轴重复自身（Galileospendulum.org，2022）。
• 接下来，“周期函数的定义域包含”所有实数值，并且“周期”运动的“值域”在“固定区间”内识别。周期，即物体在一致的运动中重复自身的时间，在整个函数的值域中被认为是一致的。

重要的周期函数

“欧拉公式”

以数学家“莱昂哈德·欧拉”的名字命名，它被认为是一个“数学公式”，有助于建立指数函数和三角函数之间的关系（Galileospendulum.org，2022）。这个公式通常用于表示“具有 2π/k 周期的特定周期”函数。

“雅可比椭圆函数”

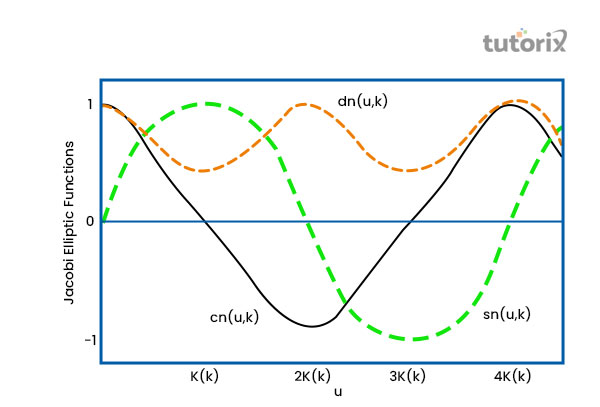
图 3：雅可比椭圆函数

这种函数的图形形状是椭圆形而不是圆形，用于求解“三角函数”（Semanticscholar.org，2022）。通过“涉及振幅和速度这两个变量”，产生了椭圆形。在描述摆的运动时，观察到使用了这些类型的函数。

傅里叶级数

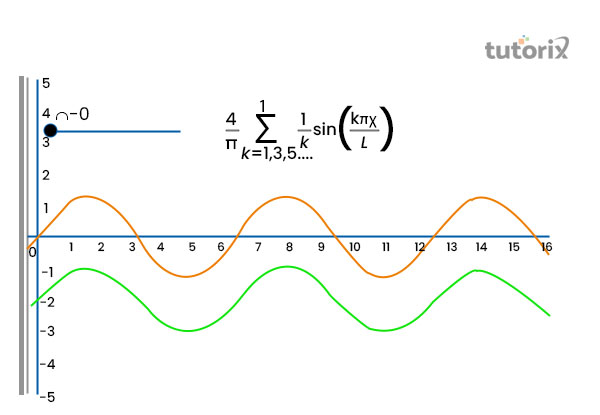
图 4：傅里叶级数

不同“周期波函数级数”的叠加导致了最强周期函数的形成，通常称为傅里叶级数。这种函数的构成通常由正弦和余弦函数进行。在热波、量子力学和振动分析的表示中，观察到傅里叶级数的应用。

周期函数的公式

为了计算周期函数，使用的特定公式是 f(x + P) = f(x)。在这个公式中，f 用于指代周期函数，其中此组件被认为是一个非零常数，由 P 表示 x 的值。另一方面，如果函数 h 扩展到所有 R，则方程将变成 h(t + 2)= h(t)（Geogebra.org，2022）。这表明方程的值取决于某些方面，例如 P 必须是实数。两个波之间经过的时间需要是恒定的。

周期函数的例子

为了找到 Tan3x + Sin5x/2 的周期，将考虑 Tanx 的周期为 π。因此，Tanx 的周期将等价于 π/3。相反，Sinx 的周期是 2π。基于此概念化，Sin5x/2 的值将等价于 2π/5/2（Analyzemath.com，2022）。

此公式将等于 4π/5 的值。根据上述找到的方程，“周期函数 f(x)= tan3x + Sin5x/2 的计算”如下

$$\mathrm{f(x)=\frac{π与4π的最小公倍数}{3与5的最大公约数}}$$

此特定计算的值将为 4π/1，这将等价于 4π。因此，在提供的方程 Tan3x +Sin5x/2 中找到的周期的最终值为 4π。

结论

本教程阐明了与周期函数相关的解释，以及“周期函数”公式的表示。人们已经看到，如果观察到实数的存在，则函数“f(x)”通常被认为是“周期函数”。“周期函数的周期”是指重复间隔的长度。除此之外，还说明了几个属性，包括周期函数需要表示实数，并且图形需要是对称的。

常见问题

Q1.周期函数中的周期是什么？

众所周知，周期函数必须包含物体的重复模式。重复模式具有与时间周期一致的图形表示，该时间周期表示每次循环之间相同类型的间隔长度。这种重复间隔的长度在周期函数中称为周期。

Q2.如何识别函数为周期函数？

在这种情况下，识别函数中观察到的重复的特定范围以及正数值的存在有助于确定方程为周期函数。根据提到的周期函数公式 f(x + T) = f(x)，需要确定 T 的值为最小值。

Q3.周期函数的相移是什么？

值的相移通常由在规则间隔内观察到的值的改变来确定。相移的实例包括正值。

Q4.周期函数的值域是什么？

人们已经观察到，周期函数包括受限值的范围。值域通常由一系列正值表示。这组值受重复的影响，以在值中实现不同的定义域。周期函数的值域是指类似的较高值。

参考文献

期刊

Zafar, A., Raheel, M., Ali, K. K., & Razzaq, W. (2020). 基于雅可比椭圆函数的新哈密顿振幅方程的光学孤子解。欧洲物理杂志 Plus，135(8)，1-17。检索自：https://www.researchgate.net

网站

Analyzemath.com，(2022)。关于周期函数。检索自：https://www.analyzemath.com/function/periodic.html [检索日期：2022 年 6 月 7 日]

Galileospendulum.org。 (2022)。关于物理量子：摆的摆动。检索自：https://galileospendulum.org/2011/05/24/physics-quanta-the-pendulums-swing/ [检索日期：2022年6月7日]

Geogebra.org， (2022)。关于傅里叶级数。检索自：https://www.geogebra.org/m/eRJ6ygyF [检索日期：2022年6月7日]

Semanticscholar.org， (2022)。关于雅可比椭圆函数和环上珠子问题的完整解。检索自：https://www.semanticscholar.org/paper/Jacobi-elliptic-functions-and-the-complete-solution-Baker-Bill/a4e6feff2f92b68b61bd8c06a4c246ecc8da19f3 [检索日期：2022年6月7日]