牵引电动机的简单电阻起动

在**简单电阻起动方法**中，牵引电动机两端的电压从零逐渐升高到额定线电压，并且通过逐渐减小外部电阻将电流保持在额定值。

假设：

• 𝑇 = 起动时间（秒）

• 𝑉 = 线电压（伏）

• 𝐼 = 恒定电流（安培）

那么，在接通电源的瞬间，电机产生的反电动势为零，并且随着电机开始旋转，反电动势立即开始建立。

在任何时刻，电机供电电压等于电机产生的反电动势加上电机串励绕组和电枢上的电压降加上起动电阻上的电压降，即：

$$\mathrm{\mathit{V\mathrm{\: =\: }E_{b}\mathrm{\: +\: }I\left ( R_{se} \mathrm{\: +\: }R_{a}\right )\mathrm{\: +\: }IR\mathrm{\: =\: }E_{b}\mathrm{\: +\: }IR_{m}\mathrm{\: +\: }IR}}$$

下图说明了牵引电动机简单电阻起动中的电压降和能量损耗。

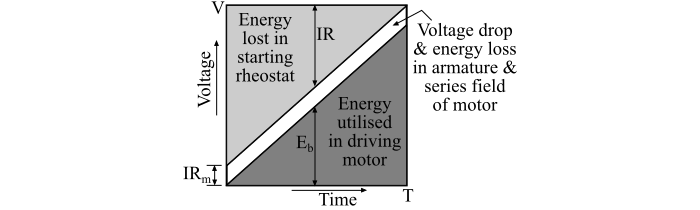
在起动结束时，外部电阻减小到零，因此外部电阻上的电压降为零，反电动势近似等于线电压，因此：

$$\mathrm{\mathit{E_{b}\mathrm{\: =\: }V-IR_{m}}}$$

因此，起动期间从电源汲取的能量为：

$$\mathrm{起动期间能量\mathrm{\: =\: }\mathit{V\times I\times T}}$$

外部电阻上的能量损耗为：

$$\mathrm{外部电阻能量损耗\mathrm{\: =\: }外部电阻平均电压降\times 电流\times 时间}$$

$$\mathrm{\Rightarrow 外部电阻能量损耗\mathrm{\: =\: }\mathit{\frac{V-IR_{m}\mathrm{\: +\: }\mathrm{0}}{\mathrm{2}}\times I\times T}}$$

如果忽略串励绕组和电机电枢上的电压降，则：

$$\mathrm{\therefore 外部电阻能量损耗\mathrm{\: =\: }\frac{1}{2}\mathit{V\times I\times T}}$$

因此，用于驱动电机的能量为：

$$\mathrm{利用能量\mathrm{\: =\: }供给能量\, -\, 外部电阻能量损耗}$$

$$\mathrm{\Rightarrow 利用能量\mathrm{\: =\: }\mathit{VIT-\mathrm{\frac{1}{2}}VIT\mathrm{\: =\: }\mathrm{\frac{1}{2}}VIT}}$$

此外，电机的起动效率为：

$$\mathrm{\eta \mathrm{\: =\: }\frac{利用能量}{供给能量}\times 100\mathrm{\: =\: }\mathit{\frac{VIT/\mathrm{2}}{VIT}}\times 100\mathrm{\: =\: }50\%}$$

Manish Kumar Saini

更新于: 2022年5月19日

586 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习