数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究C语言中奇数阶方阵中间行与中间列的乘积
给定一个方阵mat[row][column]，其中行数和列数相等且为奇数，这意味着行数和列数必须是奇数，即不能被2整除，任务是找到该矩阵中间行和中间列的乘积。
如下图所示：
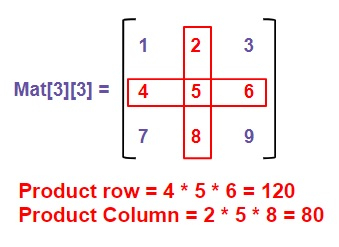
约束条件
矩阵必须是方阵。
列数和行数必须是奇数。
输入
mat[][] = {{1, 2, 3},
{4, 5, 6},
{7, 8, 9}}输出
Product of middle row = 120 Product of middle column = 80
解释
Product of middle row = 4 * 5 * 6 = 120 Product of middle column = 2 * 5 * 8 = 80
输入
mat[][] = {{3, 5, 0},
{1, 2, 7},
{9, 0, 5}}输出
Product of middle row = 14 Product of middle column = 0
解释
Product of middle row = 1 * 2 * 7 = 120 Product of middle column = 5 * 2 * 0 = 0
下面使用的方法如下，用于解决问题
将矩阵mat[][]作为输入。
从中间行和中间列遍历矩阵
计算中间行和中间列的乘积并返回结果。
算法
Start
In function int product(int mat[][MAX], int n)
Step 1→ Declare and initialize rproduct = 1, cproduct = 1
Step 2→ Loop For i = 0 and i < n and i++
Set rproduct = rproduct * mat[n / 2][i]
Set cproduct = cproduct * mat[i][n / 2]
Step 3→ Print "Product of middle row: rproduct “
Step 4→ Print "Product of middle column: cproduct”
In function int main()
Step 1→ Declare and initialize mat[][MAX] {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } }
Step 2→ Call product(mat, MAX)
Stop示例
#include <stdio.h>
#define MAX 3
int product(int mat[][MAX], int n){
int rproduct = 1, cproduct = 1;
//We will only check the middle elements and
//find their products
for (int i = 0; i < n; i++) {
rproduct *= mat[n / 2][i];
cproduct *= mat[i][n / 2];
}
// Printing the result
printf("Product of middle row: %d
", rproduct);
printf("Product of middle column: %d
", cproduct);
return 0;
}
// Driver code
int main(){
int mat[][MAX] = {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
product(mat, MAX);
return 0;
}输出
如果运行上述代码，它将生成以下输出：
Product of middle row: 120 Product of middle column: 80
更新于：2020年8月13日
203 次浏览
广告