数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学Python程序：检查机器人能否通过持续移动到已访问点到达目标
假设我们有一个机器人，当前位于(0, 0)位置（笛卡尔平面）。我们有一份机器人可执行的移动列表，包含N（北）、S（南）、W（西）和E（东）。但是，如果机器人到达之前到达过的地方，它将继续沿同一方向移动，直到到达一个新的未访问点。我们必须检查它在移动后是否会到达(x, y)坐标。
例如，输入如下：
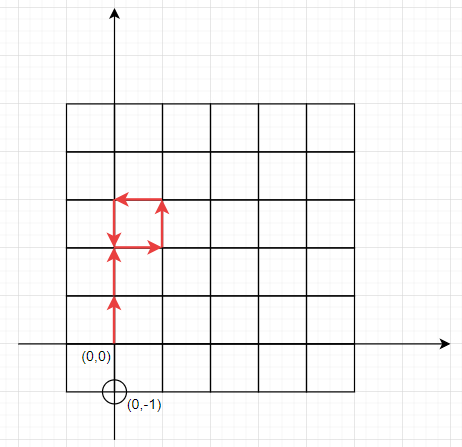
moves = ['N','N','E','N','W','S'], coord = [0, -1]，则输出为True，因为机器人将向上移动两次，向右移动一次，再次向上移动一次，向左移动一次，向下移动一次，由于当前位置已被访问，它将向下移动，然后该位置也被访问，再次向下，因此停止在(0, -1)位置。
为了解决这个问题，我们将遵循以下步骤：
ny := 0, nx := 0
l := 一个新的集合，最初插入坐标(0, 0)
对moves中的每个k，执行：
如果k等于"N"，则
当(nx, ny)在l中时，执行：
ny := ny + 1
否则，如果k等于"S"，则
当(nx, ny)在l中时，执行：
ny := ny - 1
否则，如果k等于"E"，则
当(nx, ny)在l中时，执行：
nx := nx + 1
否则，
当(nx, ny)在l中时，执行：
nx := nx - 1
将(nx, ny)添加到l
当coord等于(nx, ny)时返回true，否则返回false
让我们看下面的实现来更好地理解：
示例
class Solution:
def solve(self, moves, coord):
ny = nx = 0
l = {(0, 0)}
for k in moves:
if k == "N":
while (nx, ny) in l:
ny += 1
elif k == "S":
while (nx, ny) in l:
ny -= 1
elif k == "E":
while (nx, ny) in l:
nx += 1
else:
while (nx, ny) in l:
nx -= 1
l.add((nx, ny))
return coord[0] == nx and coord[1] == ny
ob = Solution()
moves = ['N','N','E','N','W','S']
coord = [0,-1]
print(ob.solve(moves, coord))输入
['N','N','E','N','W','S'], [0,-1]
输出
True
更新于：2020年10月21日
194 次浏览
广告