检查给定两个三角形相似度的程序

---

在这个问题中，我们将学习如何检查给定两个三角形的相似性，从程序员的角度来看，这在现实世界中有很多应用案例。

为了构建和管理物体的二维和三维模型，使用 CAD 系统，而一个关键功能是比较两个三角形的能力。

例如，从事设计和施工的工程师可能需要确保建筑物的基础测量与蓝图相符。工程师可以使用具有内置功能来检查两个三角形相似性的 CAD 工具，快速评估地基的角和边是否与布局匹配。这有助于确保建筑物的结构稳定性和安全性。

此外，三维打印技术通过 CAD 软件生成物体的三维模型。在这种情况下，相似性检查有助于确保模型打印精确并按所需比例进行。对于复杂的模型，这至关重要，因为手动验证相似性可能既繁琐又容易出错。

在机器人技术领域，程序员可以使用相似性检查工具来确保机器人运动的精度。检查两个三角形的相似性有助于确保机器人手臂（通常具有多个关节）执行的复杂运动精确且一致。

解释

现在让我们了解计算三角形相似性中涉及的一些数学知识。

如果两个三角形具有以下特征，则它们相似：

• 两个三角形的角度相等。

• 三角形的对应边具有相同的比例。

有三种方法可以确定两个三角形是否相似：SSS、SAS 和 AA。让我们简要讨论每个定理。

SSS（边边边）准则

在给定的两个三角形中，如果三对边的比例相同，则这两个三角形相似。

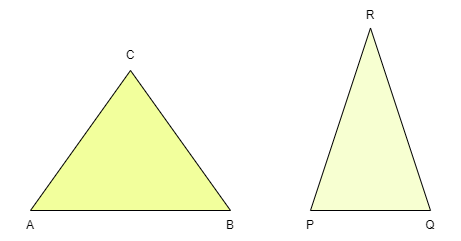
让我们考虑上面给出的两个三角形。如果三对边的比例相等，即 AC/PR = AB/PQ = CB/RQ，则上述两个三角形可以通过 SSS 准则相似。

SAS（边角边）准则

在给定的两个三角形中，如果两对边的比例相同，并且这两个边之间的角度在两个三角形中都相同，则这两个三角形相似。

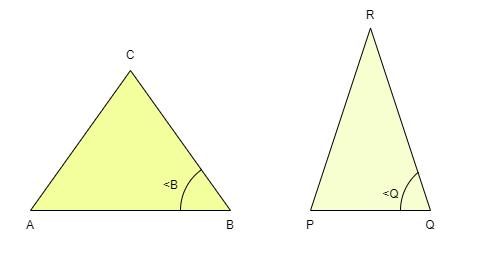
如果我们以上面的三角形为例，那么如果 AB/PQ = BC/QR 且∠B = ∠Q，则这两个三角形通过 SAS 准则相似。

AA（角角）准则

在给定的两个三角形中，如果两个三角形的任意两个角相等，则这两个三角形相似。

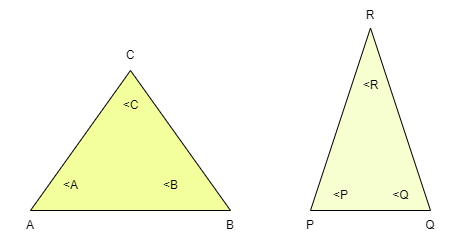
如果我们以上面的三角形为例，那么如果∠A =∠P 且∠B =∠Q，或者∠A =∠P 且∠C =∠R，或者存在任何此类组合，则这两个三角形通过 AA 准则相似。

通常，我们得到三角形三个点的坐标，然后我们需要检查相似性。在这种情况下，我们将使用此公式计算距离。

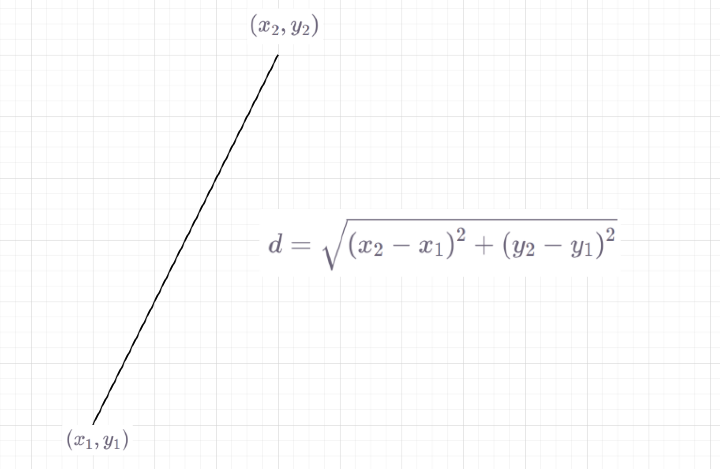
当提供坐标时，用于检查给定两个三角形相似度的程序。

方法

让我们将整个程序解码为逐步算法

• 将两个三角形三个点的坐标作为输入。

• 使用上面讨论的公式计算坐标之间的长度，即 distance= Math.sqrt(Math.pow(y2-y1,2)+Math.pow(x2-x1,2))

• 计算两个三角形所有边的长度后，计算所有对的比例。

• 接下来，检查所有三个比例是否相同，如果相同，则打印三角形相似，否则打印三角形不相似。

现在，我们将编写实现上述算法的代码

示例

当提供坐标时，用于检查给定两个三角形相似性的 C++ 程序。

#include <iostream>
#include <cmath>
using namespace std;

int main() {
   double x1 = 0, y1 = 0, x2 = 3, y2 = 0, x3 = 0, y3 = 4; //coordinates of first triangle (x1, y1), (x2, y2), (x3, y3)
   double p1 = 0, q1 = 0, p2 = 6, q2 = 0, p3 = 0, q3 = 8; //coordinates of second triangle (p1, q1), (p2, q2), (p3, q3)
   
   // calculate the distance between the coordinates of the first triangle
   double dist1 = sqrt(pow((x2 - x1), 2) + pow((y2 - y1), 2));
   double dist2 = sqrt(pow((x3 - x2), 2) + pow((y3 - y2), 2));
   double dist3 = sqrt(pow((x1 - x3), 2) + pow((y1 - y3), 2));
   
   // calculate the distance between the coordinates of the second triangle
   double dist4 = sqrt(pow((p2 - p1), 2) + pow((q2 - q1), 2));
   double dist5 = sqrt(pow((p3 - p2), 2) + pow((q3 - q2), 2));
   double dist6 = sqrt(pow((p1 - p3), 2) + pow((q1 - q3), 2));
   
   // calculate the ratio of the length of the triangle
   double ratio1 = dist1/dist4;
   double ratio2 = dist2/dist5;
   double ratio3 = dist3/dist6;
   
   // check if the ratio of all three pairs of sides of the triangle are same, we are using SSS criteria
   if ((ratio1 == ratio2) && (ratio2 == ratio3)) {
      cout << "The two triangles are similar." << endl;
   } else {
      cout << "The two triangles are not similar." << endl;
   }
   
   return 0;
}

输出

The two triangles are similar.

复杂度

时间复杂度：O(1)，因为这段代码执行的计算次数是固定的，与输入的大小无关。

空间复杂度：O(1)，因为这段代码使用固定数量的变量来存储输入值和结果，与输入的大小无关。

当提供坐标时，用于检查给定两个三角形相似度的程序。

方法

让我们将整个程序解码为逐步算法

• 将三角形的角度作为输入。

• 比较角度以检查三角形的任意两个角度是否相同，这里我们使用 AA 准则。

• 如果任意两个角度相同，则打印三角形相似，否则打印三角形不相似。

现在，我们将编写实现上述算法的代码。

示例

当提供角度时，用于检查给定两个三角形相似性的 C++ 程序。

#include <iostream>
using namespace std;

bool check_aa(int a1,int a2,int a3,int a4,int a5,int a6){
   if((a1==a4 || a1==a5 || a1==a6) && (a2==a4 || a2==a5 || a2==a6))
   return true;
   else
   return false;

}
int main(){
   
   // Input:  the angles of the triangles
   double a1 = 30, a2 = 60, a3 = 90; //angles of triangle A
   double a4 = 60, a5 = 90, a6 = 30; //angles of triangle B
   
   
   bool similar= check_aa(a1,a2,a3,a4,a5,a6);
   
   if (similar)
      cout << "The two triangles are similar." << endl;
   else
      cout << "The two triangles are not similar." << endl;
}

输出

The two triangles are similar.

复杂度

时间复杂度：O(1)，因为这段代码执行的计算次数是固定的，与输入的大小无关。

空间复杂度：O(1)，因为这段代码使用固定数量的变量来存储输入值和结果，与输入的大小无关。

结论

在本文中，我们尝试根据两种情况解释检查两个三角形相似性的方法，一种是提供边作为输入，另一种是提供角作为输入。我希望本文能帮助您更好地学习这个概念。