Python程序检查给定图是否为二分图

假设我们有一个无向图，我们需要检查该图是否为二分图。众所周知，当我们可以将图的节点分成两个集合 A 和 B，并且图中的每条边 {u,v} 都有一个节点 u 在 A 中，另一个节点 v 在 B 中时，该图就是二分图。

所以，如果输入是这样的

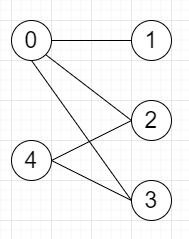
那么输出将是 True，[0,4] 在集合 A 中，[1,2,3] 在集合 B 中，并且所有边都从 A 到 B 或 B 到 A，而不是 A 到 A 或 B 到 B。

为了解决这个问题，我们将遵循以下步骤：

  • 定义一个函数 dfs()。这将获取源节点

  • 对于graph[source]中的每个顶点，执行以下操作：

    • 如果color[vertex]不等于 -1，则

      • 如果color[vertex]与color[source]相同，则

        • result[0] := False

        • 返回

      • 继续下一个迭代

    • color[vertex] := 1 - color[source]

    • dfs(vertex)

  • 从主方法中，执行以下操作：

  • n := arr的大小

  • graph := 顶点 0 到 n-1 的空邻接表

  • 对于范围 0 到 n 中的 i，执行以下操作：

    • 对于arr[i]中的每个 j，执行以下操作：

      • 将 i 插入到 graph[j] 中

      • 将 j 插入到 graph[i] 中

    • color := 一个大小为 n 的列表，并填充为 -1

    • result := 一个包含一个 True 值的列表

  • 对于范围 0 到 n 中的 i，执行以下操作：

    • 如果color[i]与 -1 相同，则

    • dfs(i)

  • 返回result[0]

让我们看看以下实现以获得更好的理解：

示例

 实时演示

from collections import defaultdict
class Solution:
   def solve(self, arr):
      n = len(arr)
      graph = [set() for i in range(n)]
      for i in range(n):
         for j in arr[i]:
            graph[j].add(i)
            graph[i].add(j)
      color = [-1] * n
      result = [True]
      def dfs(source):
      for child in graph[source]:
         if color[child] != -1:
            if color[child] == color[source]:
               result[0] = False
               return
            continue
      color[child] = 1 - color[source]
      dfs(child)
   for i in range(n):
      if color[i] == -1:
      dfs(i)
   return result[0]
ob = Solution()
graph = [[1,2,3],[0],[0,4],[0,4],[2,3]]
print(ob.solve(graph))

输入

graph = [[1,2,3],[0],[0,4],[0,4],[2,3]]

输出

True

更新于: 2020年10月5日

671 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告