数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究Python程序：查找图中的关键边和伪关键边
假设我们得到一个包含n个顶点的图，编号从0到n-1。图是无向图，每条边都有权重。因此，给定图，我们必须找到图的最小生成树中的关键边和伪关键边。如果删除该边会导致最小生成树的权重增加，则该边称为关键边。伪关键边是可以出现在所有图的最小生成树中，但并非全部出现的边。我们根据给定的图作为输入找到边的索引。
因此，如果输入如下所示：
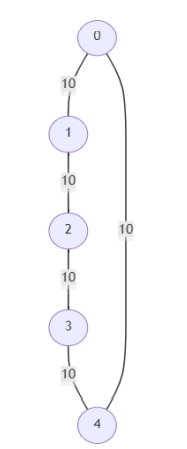
且顶点数为5，则输出将为[[], [0, 1, 2, 3, 4]]。给定图中没有关键边，所有边都是伪关键边。由于所有边的权重都相同，因此图中的任意3条边将构成一个最小生成树。
要解决此问题，我们将遵循以下步骤：
定义一个函数find_mst()。它将接收num_vertices、graph、init（默认为null）、exl（默认为null）作为参数。
定义一个辅助函数visit()。它将接收u作为参数。
k[u] := True
对于graph[u]中的每个v、w（一个空列表），执行以下操作：
如果exl不为空，并且u在exl中，且v在exl中，则：
跳过本次迭代。
如果k[v]不为True，则：
将三元组(w,u,v)推入堆tmp。
res := 0
k := 一个大小为num_arrays的新列表，所有元素都为False。
tmp := 一个新的堆。
如果init不为null，则：
u := init
v := init
w := init
res := res + w
k[u] := True
k[v] := True
visit(u) 或 visit(v)
否则，
visit(0)
当tmp不为空时，执行以下操作：
w := 从堆tmp中弹出最小元素。
u := 从堆tmp中弹出最小元素。
v := 从堆tmp中弹出最小元素。
如果k[u]和k[v]都不为零，则：
跳过本次迭代。
res := res + w
如果k[u]不为True，则：
visit(u)
如果k[v]不为True，则：
visit(v)
如果所有k都为True，则返回res，否则返回无穷大。
在主方法中，执行以下操作：
graph := 给定的图。
temp := find_mst(num_vertices, graph)。
c_edge := 一个新列表。
p_edge := 一个新列表。
对于范围0到edges的大小，执行以下操作：
如果find_mst(num_vertices, graph, exl = edges[i, index 2 to end]) > temp，则：
将i插入c_edge的末尾。
否则，如果find_mst(num_vertices, graph, init = edges[i])等于temp，则：
将i插入p_edge的末尾。
返回[c_edge, p_edge]。
示例
让我们看一下下面的实现，以便更好地理解。
from heapq import heappop, heappush
def solve(num_vertices, edges):
graph = dict()
for u, v, w in edges:
graph.setdefault(u, []).append((v, w))
graph.setdefault(v, []).append((u, w))
temp = find_mst(num_vertices, graph)
c_edge, p_edge = [], []
for i in range(len(edges)):
if find_mst(num_vertices, graph, exl = edges[i][:2]) > temp:
c_edge.append(i)
elif find_mst(num_vertices, graph, init = edges[i]) == temp:
p_edge.append(i)
return [c_edge, p_edge]
def find_mst(num_vertices, graph, init = None, exl = None):
def visit(u):
k[u] = True
for v, w in graph.get(u, []):
if exl and u in exl and v in exl:
continue
if not k[v]:
heappush(tmp, (w, u, v))
res = 0
k = [False] * num_vertices
tmp = []
if init:
u, v, w = init
res += w
k[u] = k[v] = True
visit(u) or visit(v)
else:
visit(0)
while tmp:
w, u, v = heappop(tmp)
if k[u] and k[v]: continue
res += w
if not k[u]:
visit(u)
if not k[v]:
visit(v)
return res if all(k) else inf
print(solve(5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]))输入
5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]
输出
[[], [0, 1, 2, 3, 4]]
561 次查看
